How To: Make Yin-Yang Modular Polyhedra

Last Thursday's post demonstrated how to Make Yin-Yang Pillow boxes, which were based on equilateral triangles and squares. The units for making these boxes were created by Phillip Chapman-Bell, who runs an amazing origami blog and has a spectacular flickr photostream. Using these units, you can make also make 4 of the 5 platonic solids. I made an additional template based on the regular pentagon so that the dodecahedron can be built completing the set.

I've used them in previous years as gift boxes and I suspect if made the correct size, they would make great Christmas ornaments as well.

Here are the tetrahedron, cube, and octahedron I made last night:

Below are the templates for creating the triangular, square, and pentagonal units (click to enlarge). I've included versions that show the centers of the circles if you want to use a compass to lightly etch the paper in order to fold it.

Triangle with centers of circles:

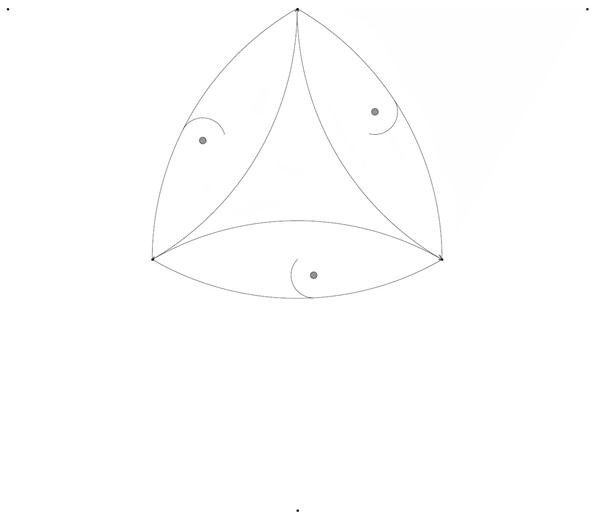
Square with centers of circles:

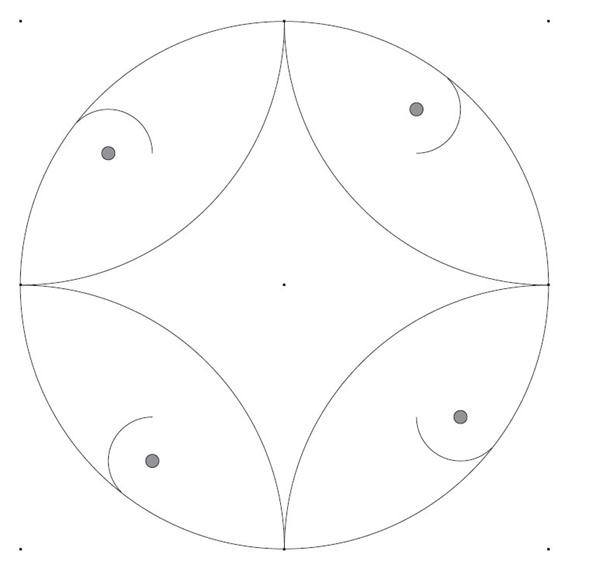
Pentagon:

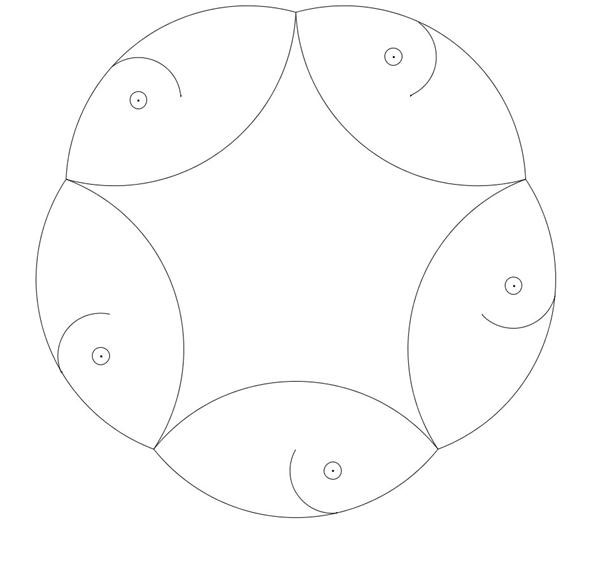
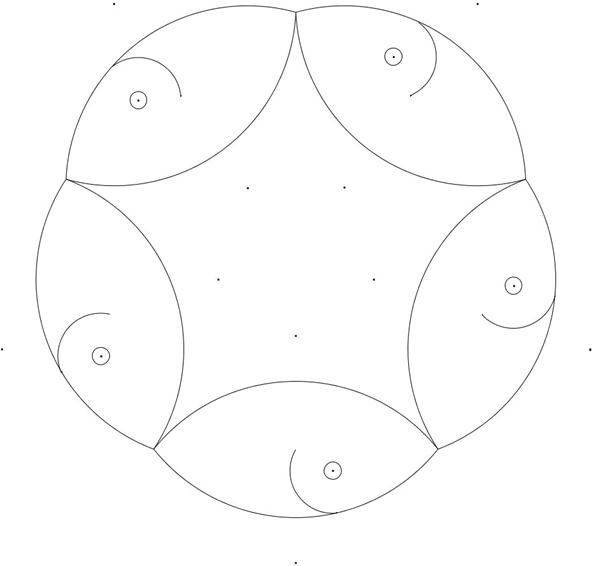
Pentagon with centers of circles:

Materials and Tools

• Paper or cardstock (2 sheets for each box, preferably in 2 different colors)
• Square box template
• Triangular box template
• Pentagonal template in pictures above
• Ball point pen (preferably non-working)
• X-acto knife

How to Curve Fold Paper

Creating the units for building the polyhedra requires paper to be folded along curves. Here is one method for folding paper in curves. 

First print out the template.

Use the pen as if you were tracing the curved lines. In this picture, I used a working pen so you can see what I am doing, but it would be better in most cases to use a non-working pen.

Now that the curve has been pre-stressed, the paper will want to fold along the curve if you apply pressure nearby by trying to fold the paper. As you fold along the curve, the entire object will bend into the third dimension.

If you do it for the other curves, it should look like this:

I actually don't usually follow this exact method for cardstock, even though it works. I usually just use my X-Acto Knife to lightly etch the curves before folding.

Math Craft moderator Imatfaal Ividya has suggested using a compass to etch the curves, so I included the centers of the circles if you would like to try that method.

How to Build a Yin-Yang Tetrahedron

Print out four versions of the triangle template. I used a paint program to color the templates and then printed them out on glossy paper.

Cut out the template making sure to cut the curved slots and the centers of the Yin-Yang pattern.  

Curve fold the unit. You will need to repeat this 3 more times to have enough units to make the tetrahedron. I suggest using different colors for each unit.

Connect two units together using the slots.

Connect a third unit as shown.

There will be a space for a fourth unit on the bottom.

How to Build a Yin-Yang Cube

I decided to make a smaller cube by re-sizing the square template so that I could print out all 6 units on one page.

Cut out and fold the units.

Now build the cube. If you use three colors like I did, you should make sure that opposite faces are the same color.

How to Build a Yin-Yang Octahedron

Again, I re-sized the templates so I could fit all 8 units required for the tetrahedron onto one sheet of paper.

Cut out and fold the units.

Connect 4 of them as shown.

The bottom should look like this:

Connect the other four units to create the octahedron. All units should be connected in rings of 4.

Using 20 triangular units, you can create the icosahedron if you connect them in rings of 5. Using 12 pentagonal units, you can create the dodecahedron.

Show Off Your Work

If you make the Yin-Yang polyhedra or any of the other previous Math Craft projects, please share with us by posting to the community corkboard. I'd love to see them adapted as ornaments and hanging on a tree. I'd also love to see them used as gift boxes. 

If you like these types of projects, let me know in the comments. If you have any other ideas you would like to pursue, let me know in the forum.