Computer Science Professor Francesco De Comité has a fantastic gallery of mathematical images on Flickr. As part of this collection, he has a few hundred images of real or rendered polyhedra made out of paper or playing cards which he calls "slide togethers." These are constructed by making cuts and then sliding one component into the other, creating a shape without using any glue. He constructed the entire set of the platonic solids—the cards form their edges—which can be seen in the image below.
I became intrigued by these and had to figure out how to make them myself. Francesco did leave some templates and other clues behind.
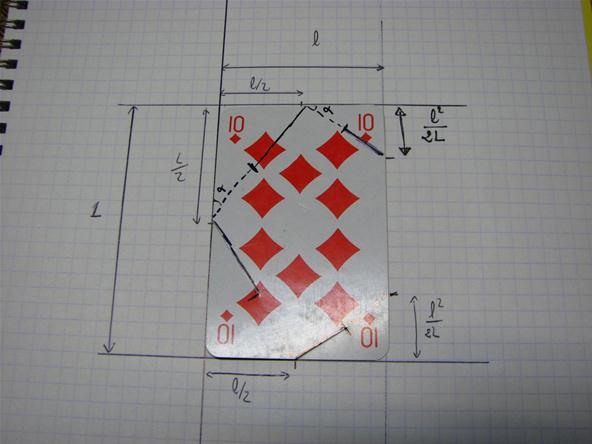
Using some creativity and trigonometry, I managed to construct my own templates and my own set.
Note: The second from the right isn't a platonic solid. It's a truncated icosahedron, and you can see how to make one of those in my other post.
Here's a downloadable template for the platonic solids so you can construct your own set. I recommend making the cube for ease of use and coolness factor. I would also recommend the dodecahedron. The others are great, but the aforementioned two are my favorites. Here's a short little tutorial on how to construct them.
Materials
- Playing cards (the constructions and number of cards required are: 6 cards for the tetrahedron, 12 cards for the cube, 12 cards for the octahedron, 30 cards for the dodecahedron, and 30 cards for the icosahedron)
- Downloadable template
- Scissors or X-Acto knife
- Cutting mat or board if using an X-Acto knife
Step 1: Download and Print the Template
Download the template by clicking on the link above. Once you're in Google Docs, go to the upper left-hand corner, and click on "File" and then "Download". Print the PDF scaled at 100%. Do not leave the scaling at "Fit on Page". This will not work.
Alternatively, click on "File" and then "Print PDF" in the Google Docs menu if you don't want a local copy. Again, remember to change the scaling to 100%.
Step 2: Use the Template to Make Cuts in the Playing Cards
Cut out the template card. You should try to cut down the center of the line. Small errors shouldn't matter much to the end product.
Place the template as perfectly as possible on top of the playing card, and cut through the template and card on the marked lines, making sure that the template doesn't move relative to the card. (Note: when cutting the cards make sure to always cut either the front or the back of the card. It doesn't matter which one you choose, but you must be consistent by either choosing the front or back.)
You can see the card behind the template.
Showing the slots cut out on the card.
Repeat until you have enough identical copies to make the desired polyhedra.
Step 3: Begin Placing the Cards
Using the slotted cards, slide one card into the other. For the tetrahedron, cube, and dodecahedron, you should always have 3 cards coming together to form a point. For the octahedron, there should be 4 cards together to form a point. For the icosahedron, there should be 5 cards coming together to form a point. Putting the last card together at the point is always the hardest part because you have to slide two different slots into each other at the same time.
Placing the first card, shown below. (Note: You could decide to have the patterned side up instead of the face. Whatever you choose, you must be consistent.)
Placing the second card forming the full vertex (point) for the tetrahedron, cube, or dodecahedron.
For the octahedron, it would look like this (4 to a vertex):
For the icosahedron, it would look like this (5 to a vertex):
After you form one point, just continue making more points at the other ends of the cards. This will result in a polyhedral ball. If it starts looking lopsided, you probably miscounted.
Forming the second vertex for a cube:
Forming vertexes so you get a square in the middle for a cube (at this point it finally begins to stabilize!):
The cube is done!
Step 4: Show Off Your Work!
You've finished making the platonic playing card "slide together"! Now you need to figure out what to do with it. Be sure to post up a picture to inspiration section! We'd love to see it.
Just updated your iPhone to iOS 18? You'll find a ton of hot new features for some of your most-used Apple apps. Dive in and see for yourself:
25 Comments
its like looking through a kaleidoscope but in real life
I hadn't thought about that but the symmetries you see are pretty similar to what you would see in a kaleidoscope.
If I get a deck with two jokers I can make the icosahedron, the cube, and the octahedron with no cards left over. Having extra cards left over would drive me crazy.
I went with the opposite approach. I bought a 12 pack of decks at Costco and now have to figure out what to build with all of the cards!
My first thought were that you could do other kinds of figures like a twister.
Then I thought about making lamps, especially the PH artichoke
http://www.google.com/search?q=ph+artichoke&tbm=isch
Oooh. That is a pretty cool lamp. That could actually work with the cards and some other structure that the cards fit into. Hmmm.... I think you just added a project to my list. Thanks!
If you got a novelty hole punch in an interesting shape – maybe smaller, nested squares – and punched out that shape from the cards, and stuck a little lightbulb in there, the light would project out through the little shapes you made too, and I think it would be pretty.
You could make something approximating the E8 lie group (depending on how many smaller squares you could cut out from the cards) as a night light! (Sorry, I love nightlights :)
To create a sturdy object, would you suggest applying glue? Or are the slits enough?
For these the slits should be enough. The tetrahedron, cube, and dodecahedron with the 3 fold vertices are quite strong. The octahedron is a little less strong, and the icosahedron is a little less due both to its size and its 5 fold vertices.
I did it Cory...template worked out real cool, here are the first 3 so much fun to make and play with (also considering I'm a No limit Hold Em Phreak these days/ I also like hallucinogens..hey) dig Frosty The Snowman https://www.facebook.com/media/set/?set=a.2466360867964.2137816.1520550546&type=1
Awesome John! Unfortunately I can't see those images. Could you post them on the corkboard here?
https://www.facebook.com/media/set/?set=a.2466360867964.2137816.1520550546&type=1#!/photo.php?fbid=2466361107970&set=a.2466360867964.2137816.1520550546&type=3&theater
If you believe in magic then nothing is out of reach
have you figured out the math for the five intersecting tetrahedrons ?
I am still working on it.
http://www.flickr.com/photos/fdecomite/5624549449/in/set-72157622365424793
http://www.flickr.com/photos/fdecomite/5625131610/in/set-72157622365424793/
those are amazing. Are they yours?
This is so cool!
nah, a math professor, he leaves clues how to make them, and I have been able to figure out parts of the math. but where ever he is, the playing cards are a different size, vs the u.s. so I am having issues, so I have not been ready to give it a try yet, plus apparently they one I am trying is pretty hard.
they're awesome looking.
I made this from http://www.georgehart.com/cards/cards.html
http://farm8.staticflickr.com/7034/6688762543_15a541549d_z.jpg
http://farm8.staticflickr.com/7172/6688766385_56e52a0e71_z.jpg
The professor Francesco De Comité got back to me with something new from his computer. It does explain why I could never get the math right. I was trying to do it with pen, paper, and self taught trig. so I am going to try to make this next once I resize everything and make a template. Then we are going to share it so other people can make them to. I was up last night around 3-6 last night since it was the middle of the day for him. this is next
http://farm6.staticflickr.com/5067/5624549449_4fb80de894_b.jpg
Cool. Looking forward to seeing how to do it. I only know how to make the platonic and archimedean solids using the math that I've figured out....which is probably more complicated than it needs to be. :)
I have just bought 30 sheets of 2400 x 1200 12mm ply... I am going to build an Icosahedron hut. Will post the results...
wow. That will be pretty awesome! I'd just like to point out that it is the angles that matter with these slide togethers and that the slits should go half way to the other edge.
hi cory... just be measuring up for the c and c machine to cut each sheet EXACTLY... and I have thought of a minor issue, you might be able to help me with... With the cards, not being very think there is no problem with the angle of the cut between the top and bottom surfaces. However with 12mm ply, there is obviously going to be an angle to cut, which is what you were hinting at above... So, the questions are these.... Are all the angle son the cuts the same? And if they are.... What would the angle be? Thanks in advance, Mark
You are right for sure...but I don't really know the answer. The angles should all be the same...so perhaps you could do some test cuts and then set the angle. I've always calculated all the angles using "simple" trigonometry but without spending a lot of time thinking about it your angle calculation gets pretty complicated. You could probably get a really good guess by building the card model and looking at the angle that was formed...and then do some tests.
I made the icosahedron for a project. I have to say how many vertices, faces and edges it has. Not sure if I need to take into consideration the corners sticking out of it. Can anyone help me?
Share Your Thoughts