How To: Create Parabolic Curves Using Straight Lines

Curve stitching is a form of string art where smooth curves are created through the use of straight lines. It is taught in many Junior High and High School art classes. I discovered it when my math students started showing me the geometric art they had created.

The process of curve stitching can be done with a piece of paper and a ruler, or anything you can make a straight line with. It is common to do these with strings as the lines. Below are a few examples of string art.

Here's an interesting one of an Isometric Cube by Lionel Deimel (who has more awesome designs on his curve stitching page).

Here's one by Eli Hess using ropes and trees. The curve formed is a parabola.

One of the easiest curves to create using curve stitching is a parabola. The straight lines do not actually create the curve, they merely approximate it. The parabola is the envelope of the straight lines. This mathematical paper proves that the curve formed by the method below is a parabola. Once a parabolic section has been created, you can use it to form interesting designs. Four of the designs above only use parabolic sections.

Materials and Tools

• Paper
• Ruler
• Pencil or Pen

Create a Parabola from Lines and a Right Angle

Draw a right angle and mark two lines of equal length at equal intervals. It should look like you are making a coordinate plane to graph an equation.

Draw a line from the farthest mark from the right angle on one line, to the closest mark to the right angle on the other line.

Now connect the 2nd farthest mark to the 2nd closest mark.

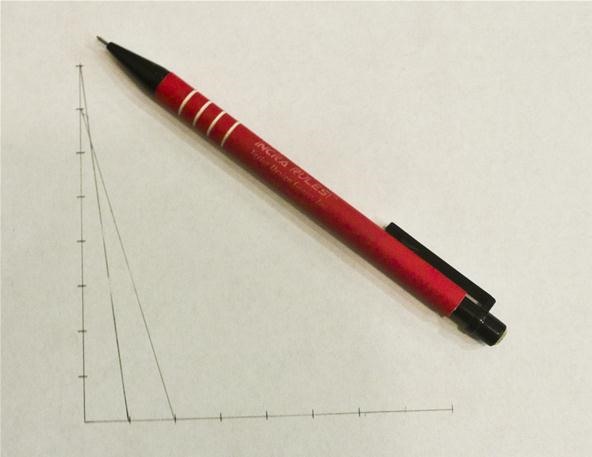
Continue connecting lines between the points as you step down one line and step up the other.

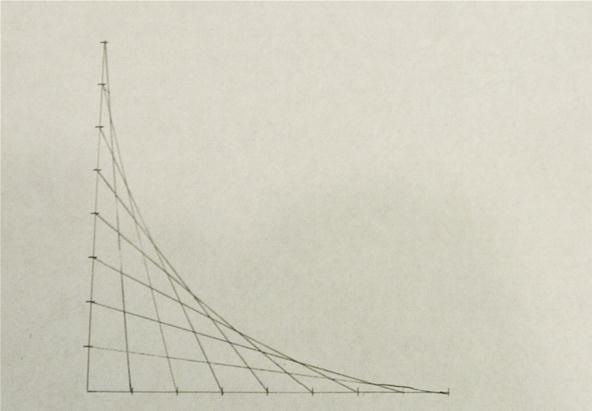
Here I've rotated the image 45 degrees so the parabola is oriented in the conventional way.

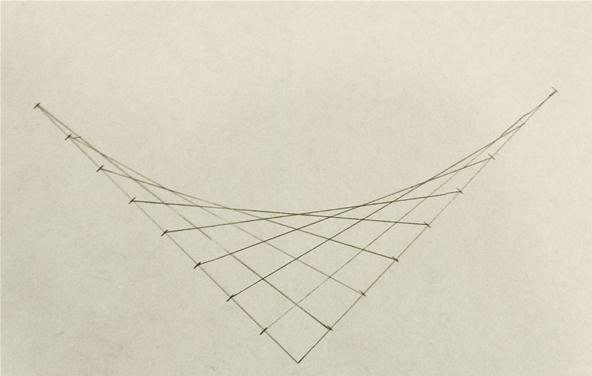
The curve was pretty smooth looking with eight marks on each line, but can be made smoother by adding more marks. There are 32 in this picture.

If you want the parabola to continue, you can extend the lines both beyond the right angle.

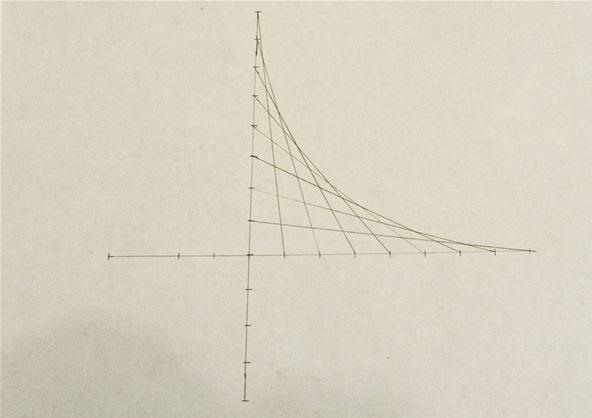
If you want the parabola to continue getting steeper, you can extend the marks past the right angle and connect them up as shown below. Remember to count the right angle as a mark.

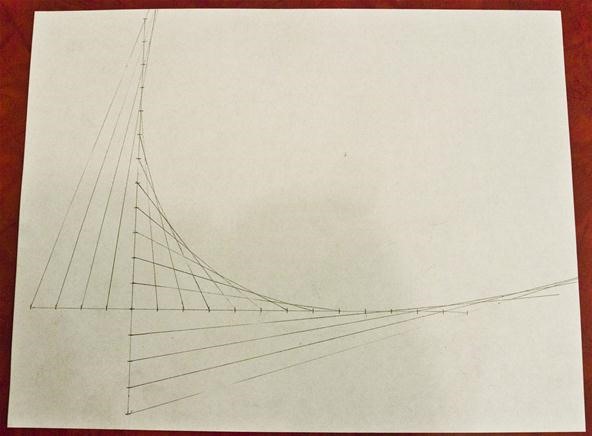
Making Narrower or Wider Parabolas by Using Non-Right Angles

If you want a narrower parabola, you can follow the process above, but use an angle less than 90 degrees. The angle below is 45 degrees.

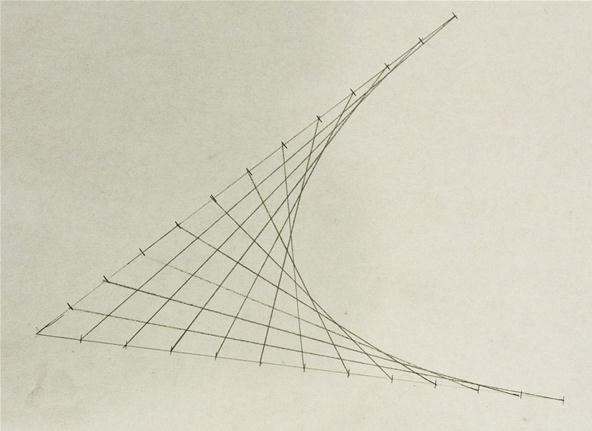
If you want a wider parabola, you can follow the process above, but use an angle greater than 90 degrees. The angle below is 120 degrees.

Creating Parabolic Sections Inside Polygons

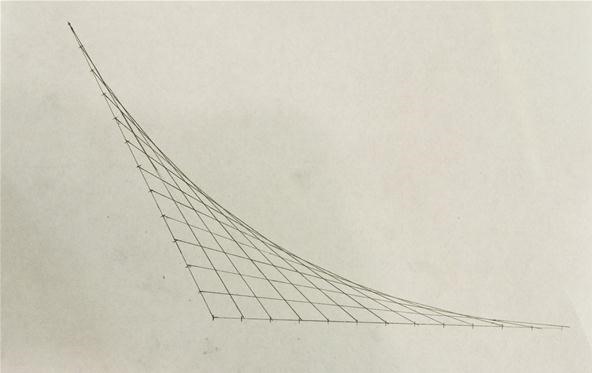
Since the process of creating parabolic sections can be done with any angle, you can use angles that make polygons and use the process on all of the sides. Using the process on regular polygons where all of the angles and sides are the same results in pleasing figures. I constructed a regular triangle below, but the process would work for any regular polygon. You could just find an image of a regular polygon using google image search and use that.

Connect the sides of your regular polygon using lines as in the process above.

After all three sides have been connected.

The path that has been created by the straight lines actually follows the outline of a trefoil knot which was explored in a previous post on torus knots.

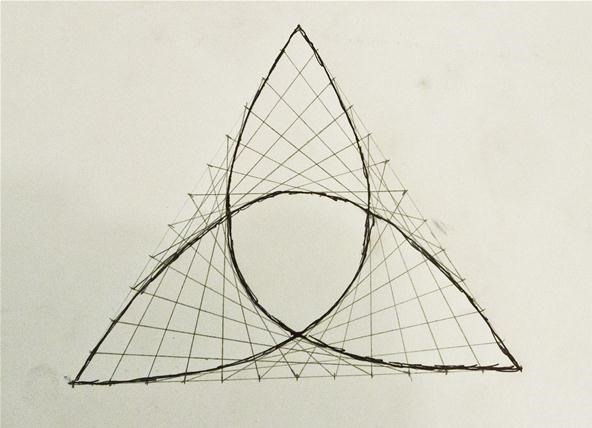
Creating Star Figures from Parabolic Sections

If you use the lines that connect up the center of a regular polygon to each of the sides, you get star figures made out of your parabolas. The image below used a pentagon, which has 5 central angles of 72 degrees.

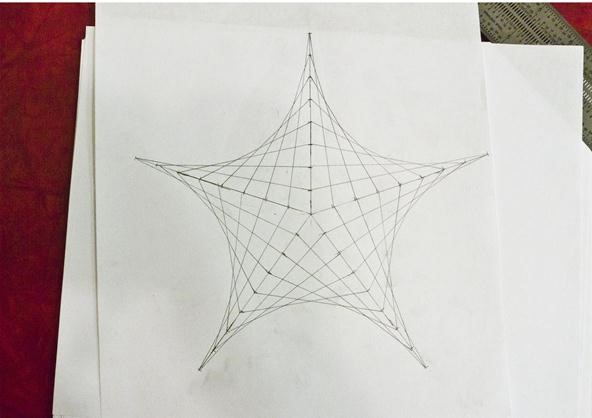
This reminds me of a three dimensional version I made out of pencils. Perhaps we'll explore how to do something similar to this process in 3d in a later post.

Combine Parabolic Sections to Make a Work of Art.

There are an infinite number of ways to combine these parabolic sections to create interesting figures. I am not a very good artist, but here are a few pieces I have made, plus some ideas for creating your own.

Embedding parabolic curves of smaller sizes can make an interesting self-similar fractal pattern.

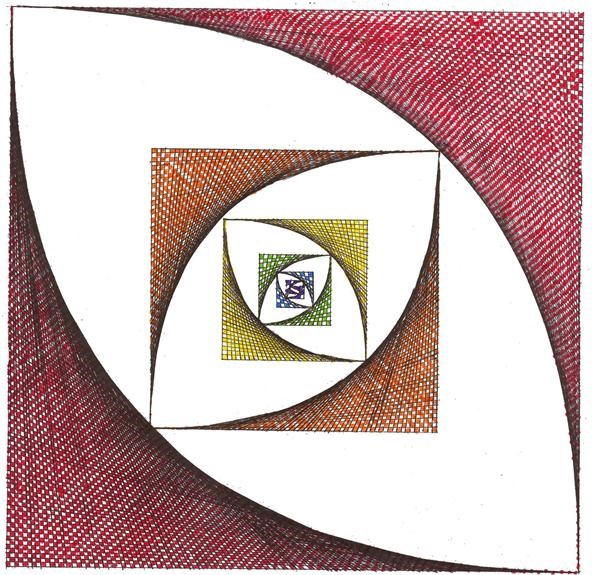
Combing the polygons or star figures into tilings regular tilings of the plane. This one uses star figures based off of the square. Note: It is much easier to use a computer to do this.

Here's one using triangles to tile the plane. Note the strong connections between triangles, circles, and hexagons that you can see in the image below.

There are tilings that use multiple polygons to tile the plane. Here's a semi-regular tiling that uses triangles, squares, and hexagons. I created a version of each figure by hand, and then copied them using Photoshop.

You can use lines of different colors to create your parabolic sections.

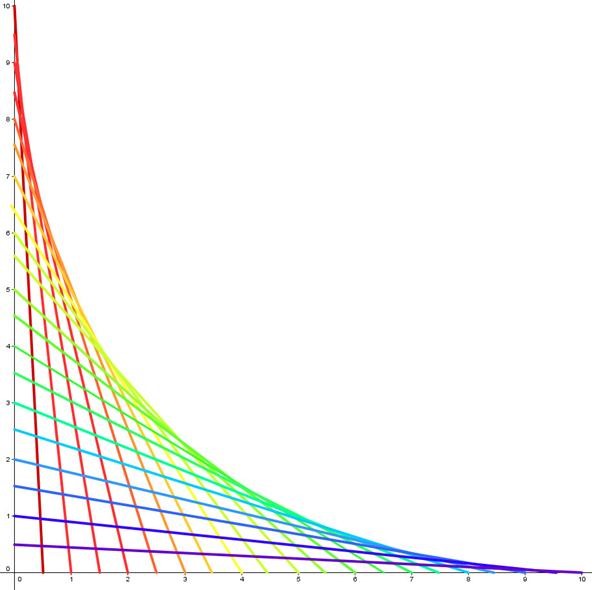
You can copy and overlay these sections using a program like Photoshop. There's an infinite number of eye-pleasing combinations.

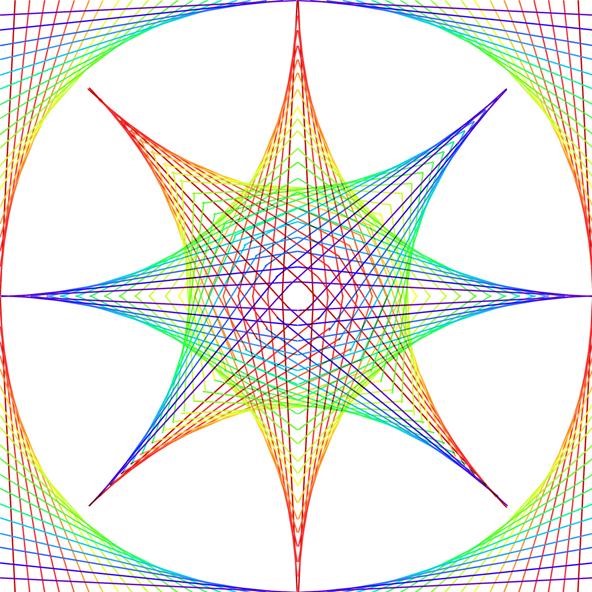
Show Off Your Parabolic Artwork

If you make any of these designs or any of your own, let us know by posting a picture or video up on the corkboard. We'd love to see them. Can anyone make them using other materials?

On Thursday, we'll look at creating some curves from straight lines using a circle as the starting point. We'll be able to create concentric circles, ellipses, and cardioids, among others.