Math Craft How-Tos


How To: Make a 'Flex Mex'—A Mathematically Delicious Hexaflexagon Burrito
Here's a great excuse to play with your food—and learn some math while you're at it. We've all seen a hexaflexagon folded out of paper, but how about a burrito? Vi Hart, a "mathmusician" over at the Khan Academy, came up with the Flex Mex, a burrito folded into a hexaflexagon with all the toppings inside. The spreadable ingredients (guacamole, sour cream and salsa) go inside the folds, then it's topped with beans and cheese.

How To: Holy String Art, Batman! 6 of the Coolest Thread Art Projects Ever
You may remember string art from your elementary school days. If so, it probably makes you think of the 2D geometrical designs that took every ounce of patience you had as a kid. Or those laborious curve stitch drawings, which string art was actually birthed from. But thanks to some innovative modern artists, string art has gotten a lot more interesting. Here are some of the most creative applications so far.

How To: Design Your Own Playing Card Sculpture
Download the Software Go to the Antiprism downloads page. Download and install Antiprism 0.20.

How To: Make Yin-Yang Modular Polyhedra
Last Thursday's post demonstrated how to Make Yin-Yang Pillow boxes, which were based on equilateral triangles and squares. The units for making these boxes were created by Phillip Chapman-Bell, who runs an amazing origami blog and has a spectacular flickr photostream. Using these units, you can make also make 4 of the 5 platonic solids. I made an additional template based on the regular pentagon so that the dodecahedron can be built completing the set.

How To: Make Icosahedral Planet Ornaments
In honor of the new Astronomy World, I thought we should look at a few planetary icosahedrons. The icosahedron is the most round of the Platonic solids with twenty faces, thus has the smallest dihedral angles. This allows it to unfold into a flat map with a reasonably acceptable amount of distortion. In fact, Buckminster Fuller tried to popularize the polyhedral globe/map concept with his Dymaxion Map.

Math Craft Monday: Community Submissions (Plus How to Make Escheresque Tessellated Cubes)
It's once again Monday, which means it's time to highlight some of the most recent community submissions posted to the Math Craft corkboard. Since two of these posts were on polyhedral versions of M.C. Escher's tessellations, I thought we'd take a look at building a simple tessellated cube based off of imitations of his imagery.

How To: Make Yin-Yang Pillow Boxes
Here's a Math Craft project that takes less than 20 minutes, has an attractive, practical result, and is at least a little mind-blowing due to folding along curves.

How To: Make Nested Cube and Octahedron Boxes
These boxes are inspired by a comment from Imaatfal Avidya on a corkboard post on Platonic polyhedra from sonobe units. Imaatfal was commenting about how the cube and octahedron are related to each other.

How To: Fold a Pentakis Dodecahedron
Math Craft admin Cory Poole provided quite a few recipes for sonobe models in his blog, and I followed one to make the pentakis dodecahedron here.

Math Craft Monday: Community Submissions (Plus How to Make a Modular Origami Intersecting Triangles Sculpture)
It's once again Monday, which means it's time to highlight some of the most recent community submissions posted to the Math Craft corkboard. I also thought we'd take a look at building a model that has appeared in numerous posts. It's the simplest of the intersecting plane modular origami sculptures: The WXYZ Intersecting Planes model.

How To: Make 6-Sided Kirigami Snowflakes
We've all made them. I remember making hundreds of paper snowflakes when I was in elementary school. You take a piece of paper and fold it in half, then fold it in half again. You now have a piece that is one fourth the size of the original. Now you fold it in half diagonally. You then cut slices out of the edges of the paper, and unfold to find that you have created a snowflake. The resulting snowflake has four lines of symmetry and looks something like this: If you fold it in half diagonall...

How To: Make a Hyperbolic Paraboloid Using Skewers
In Monday's post, we created a sliceform model of a hyperbolic paraboloid. In today's post, we will create a similar model using skewers. The hyperbolic paraboloid is a ruled surface, which means that you can create it using only straight lines even though it is curved. In fact, the hyperbolic paraboloid is doubly ruled and is one of only three curved surfaces than can be created using two distinct lines passing through each point. The others are the hyperboloid and the flat plane.

Math Craft Monday: Community Submissions (Plus How to Make a Sliceform Hyperbolic Paraboloid)
It's Monday, which means once again, it's time to highlight some of the most recent community submissions posted to the Math Craft corkboard. I also thought we'd take a look at building a sliceform model of a hyperbolic paraboloid.

How To: Make a Sonobe Jasmine Dodecahedron
Math Craft admin Cory Poole posted instructions on How to Make a Cube, Octahedron & Icosahedron from Sonobe Units, plus some great complex models in his article, How to Make a Truncated Icosahedron, Pentakis Dodecahedron & More. These models use the standard sonobe unit and a coloured variant.

How To: Make Fractal Cupcakes
Last post, we looked at fractal cookies based off of the recipe by Evil Mad Scientist Laboratories. In this post, we'll follow their recipe for fractal cupcakes based off of the Koch Snowflake, which we used previously to decorate pumpkins for Halloween.

How To: Anybody Know How to Make This?
Via gurmeet.net

How To: Make Sierpinski Carpet Cookies
Since it is now the holiday season, I thought we could spend this weekend making some baked goods that have mathematical patterns on them. In this post, we'll look at making cookies that have a fractal pattern based off of a modification of the pixel cookie technique.

Math Craft Monday: Community Submissions (Plus How to Make a Magic Square Tetraflexagon)
It's Monday, which means once again, it's time to highlight some of the recent community submissions posted to the Math Craft corkboard. In this post, we'll also make a flexagon, which is a type of transformable object.

Modular Origami: How to Make a Truncated Icosahedron, Pentakis Dodecahedron & More
Last post, the Sonobe unit was introduced as a way to use multiple copies of a simply folded piece of paper to make geometric objects. In this post, we are going to explore that concept further by making two more geometric models. The first is the truncated icosahedron, which is a common stitching pattern for a soccer ball. The second was supposed to be the pentakis dodecahedron, but through systematic errors last night, I actually built a different model based off of the rhombic triacontahed...

Modular Origami: How to Make a Cube, Octahedron & Icosahedron from Sonobe Units
Modular origami is a technique that can be used to build some pretty interesting and impressive models of mathematical objects. In modular origami, you combine multiple units folded from single pieces of paper into more complicated forms. The Sonobe unit is a simple example unit from modular origami that is both easy to fold and compatible for constructing a large variety of models. Below are a few models that are easy to make using this unit.

Math Craft Monday: Community Submissions (Plus How to Make an Orderly Tangle of Triangles)
It's Monday, which means once again, it's time to highlight some of the recent community submissions posted to the Math Craft corkboard. I also thought that we'd try and create something known as an "Orderly Tangle" or "Polylink".
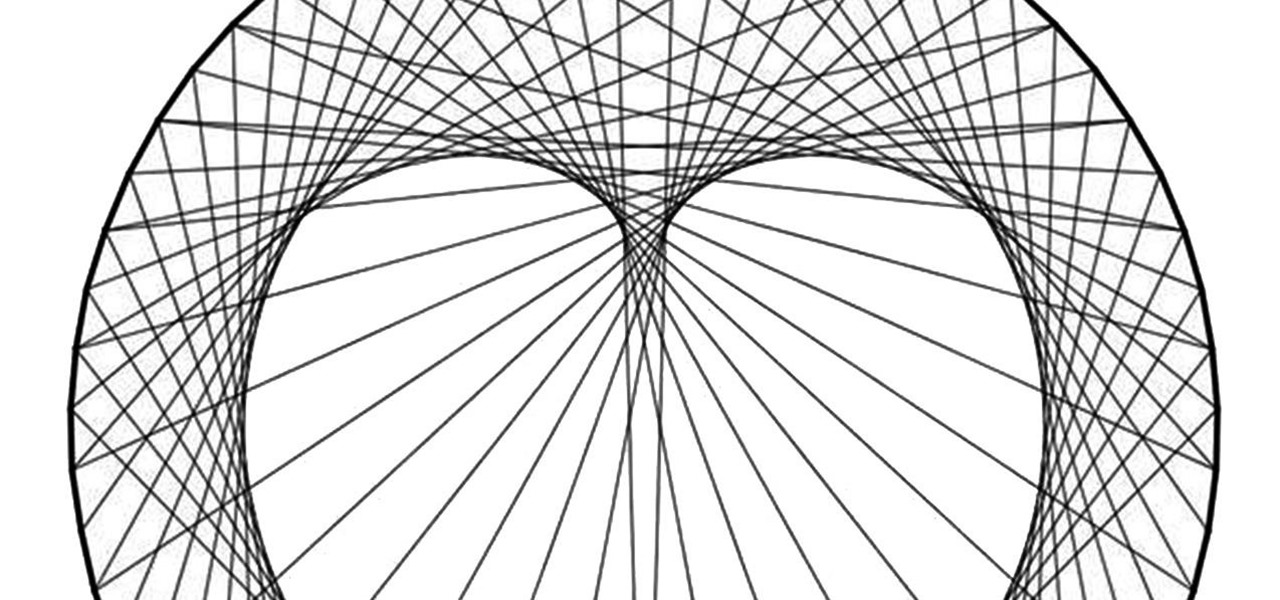
How To: Create Concentric Circles, Ellipses, Cardioids & More Using Straight Lines & Circles
Using only a circle and straight lines, it's possible to create various aesthetic curves that combine both art and mathematics. The geometry behind the concentric circle, ellipse, and cardioid dates back centuries and is easily found in the world around us. From an archery target to an apple, can you name these geometric shapes?

How To: Create Parabolic Curves Using Straight Lines
Curve stitching is a form of string art where smooth curves are created through the use of straight lines. It is taught in many Junior High and High School art classes. I discovered it when my math students started showing me the geometric art they had created.

Math Craft Monday: Community Submissions (Plus How to Make Mobius Strips)
It's another Monday, which means once again, it's time to highlight some of the recent community submissions posted to the Math Craft corkboard. Additionally, I thought we'd take a look at the Mobius Strip.

How To: Make Torus Knots from Soft Metals
Torus knots are beautiful knots formed by wrapping a line around a torus and tying the ends together to form a loop. The resulting knot has a star-like appearance when viewed from above. The 36 examples with the least number of crossings can be seen at the Knot Atlas's page on torus knots.

How To: Make Knot Sculptures from Soft Metals
In mathematics, a knot is a closed circle in a three-dimensional space that crosses itself multiple times. Since it is closed, it has no ends to tie, meaning you can't actually create such a knot. However, if you tie the ends together after you create a knot in the standard way, you will have something that is close to the mathematical description. In this post, we will explore the creation of mathematical knot sculputures using copper tubing and solid solder wire.

How To: Carve Fractals and Stars on Pumpkins
Fractals and stars are two of the most beautiful and complicated-looking classes of geometric objects out there. We're going to explore these objects and how to carve them on a pumpkin. Unlike the last one on carving polyhedral pumpkins, where we used the entire pumpkin to carve a 3 dimensional shape, the pumkin carving in this post will involve two-dimensional images on a small part of the pumpkin's surface.

How To: Carve Polyhedral Pumpkins
Halloween is coming up, so many of you may have a need or desire to carve a pumpkin and turn it into a Jack O' Lantern. This week we are going to explore carving our pumpkins into interesting geometric shapes. In this post, we will carve the pumpkins into spherical versions of polyhedra, and in Thursday's post we will carve 2 dimensional stars and some simple fractal designs into the pumpkins.

You Won't Believe They Roll: How to Build Half Circle and Elliptical Wobblers
If you thought the last post on Two Circle Wobblers was wild, then wait until you see what happens when you build wobblers out of two half circles or two ellipses. In both of these cases, the center of gravity still remains constant in the vertical direction, allowing them to roll down the slightest of inclines or even travel a significant distance on a level surface if given a push or even when blown on.

How To: Make a Two Circle Wobbler from CDs
One of my favorite simple projects is building two circle wobblers. I love how such a simple object amazes with its motion. The two circle wobbler is an object made out of two circles connected to each other in such a way that the center of mass of the object doesn't move up or down as it rolls. This means that it will roll very easily down a slight incline. It will also roll for a significant distance on a level surface if you start it by giving it a small push or even by blowing on it!
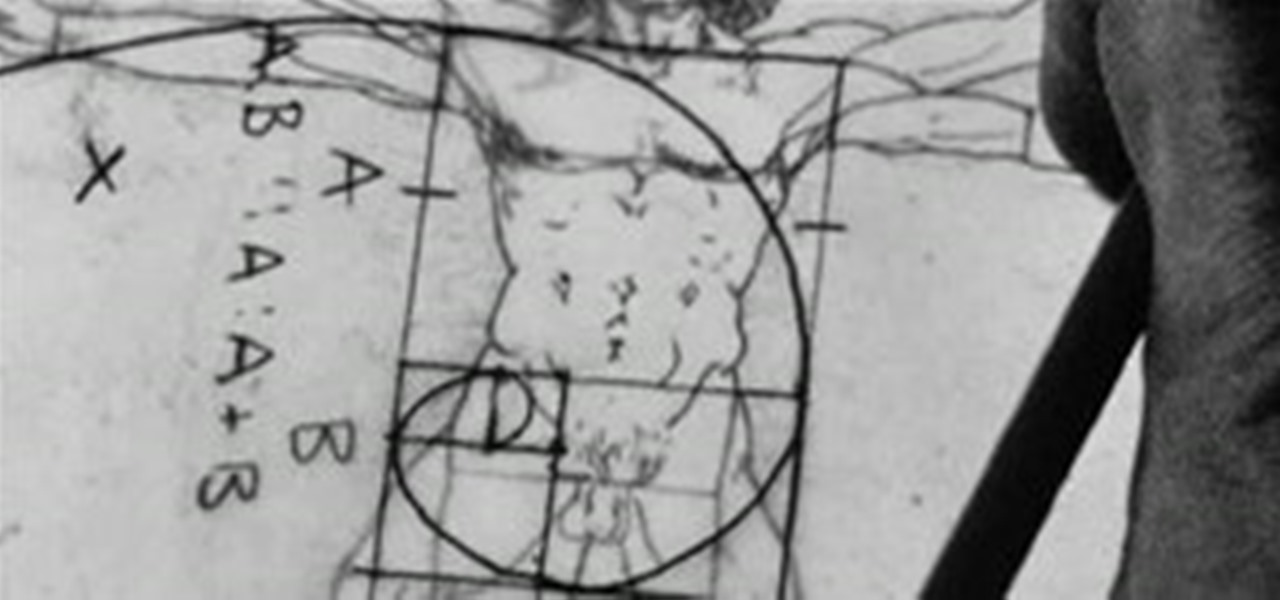
Math Craft Monday: Community Submissions (Plus How to Make the Golden Spiral)
It's Monday, time to highlight some of the community submissions posted to the Math Craft corkboard. One of these posts inspired me so much, I think it merits a closer look. Today, I present a "simple" method for making a golden spiral using just a straight edge, a compass, and a template, inspired by RJ Ellicock's golden ratio post.

How To: Make the Platonic Solids Out of Playing Cards
Computer Science Professor Francesco De Comité has a fantastic gallery of mathematical images on Flickr. As part of this collection, he has a few hundred images of real or rendered polyhedra made out of paper or playing cards which he calls "slide togethers." These are constructed by making cuts and then sliding one component into the other, creating a shape without using any glue. He constructed the entire set of the platonic solids—the cards form their edges—which can be seen in the image b...

How To: Welcome to Math Craft World! (Bonus: How to Make Your Own Paper Polyhedra)
Welcome to Math Craft World! This community is dedicated to the exploration of mathematically inspired art and architecture through projects, community submissions, and inspirational posts related to the topic at hand. Every week, there will be approximately four posts according to the following schedule:


