Home

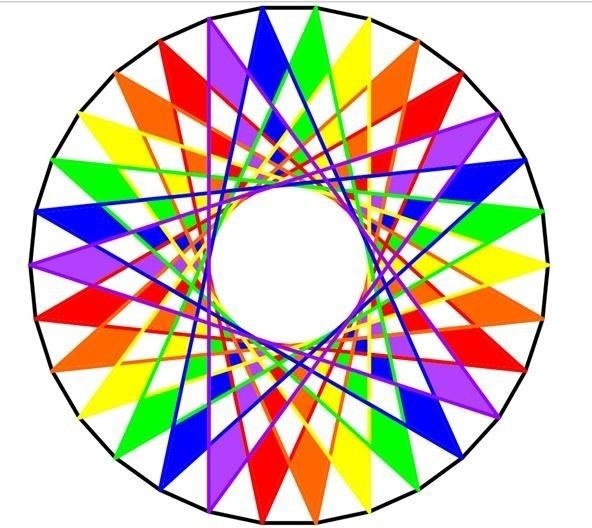
How to Create Concentric Circles, Ellipses, Cardioids & More Using Straight Lines & Circles

Mar 10, 2012 12:50 PM

Aug 30, 2017 01:55 AM

Using only a circle and straight lines, it's possible to create various aesthetic curves that combine both art and mathematics. The geometry behind the concentric circle, ellipse, and cardioid dates back centuries and is easily found in the world around us. From an archery target to an apple, can you name these geometric shapes?

You will by the end of this step-by-step tutorial, and you'll also be ready to try your hand at some geometric art yourself, which you could then spin into op art or string art. To create the curve examples that follow, I used a pencil, ruler, and protractor to mark off degrees and keep things exact. If you want, you could even use the free computer program GeoGebra to draw concentric circles, ellipses, and cardioids.

Geometric design with circular patterns and a red pen.

Concentric circles (top), ellipse (bottom left), and cardioid (bottom right).

Diagram illustrating the reflection of light rays in a parabolic shape.

Cory Poole/WonderHowTo

Geometric diagram of a circle with radial lines.

Cory Poole/WonderHowTo

Concentric circles (top), ellipse (bottom left), and cardioid (bottom right).

Cory Poole/WonderHowTo

Materials & Tools Needed

For all of these curves, we'll need a few basic geometry tools and drawing utensils.

paper
ruler or straight edge
pen or pencil
compass for drawing circles (or images of circles or regular polygons)
protractor (for marking off precise degrees)

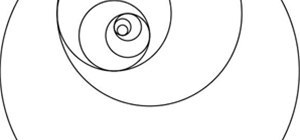
Option 1. Making Concentric Circles

Concentric circles are circles that share a midpoint, such as an archery target or a dartboard. The circles, though different size, all have the same bullseye. Regular polygons, regular polyhedra, and spheres can also be described as concentric as they all share the same center. In fact, in our first example below, we create a concentric circle by drawing polygons:

Mark a Circle at Even Intervals

This circle is marked every 10 degrees, so 36 marks total:

Circle with measurement markings and protractor.

Cory Poole/WonderHowTo

Connect One Mark to Another

The number of marks skipped will determine the size of the concentric circle created. I chose to skip eight:

Red pen placed next to a circular protractor on a sheet of paper.

Cory Poole/WonderHowTo

Create Lines All the Way Around the Circle

Take the next mark and connect it to the mark ahead of the one you connected the previous one to. Continue doing this.

Based on your first mark, take the next mark and connect it to the mark ahead of the one you connected the previous one to, then continue doing this:

Red pencil resting on a paper circle with radiating lines.

Cory Poole/WonderHowTo

Geometric drawing of a circular shape with radiating lines, accompanied by a red pencil.

Cory Poole/WonderHowTo

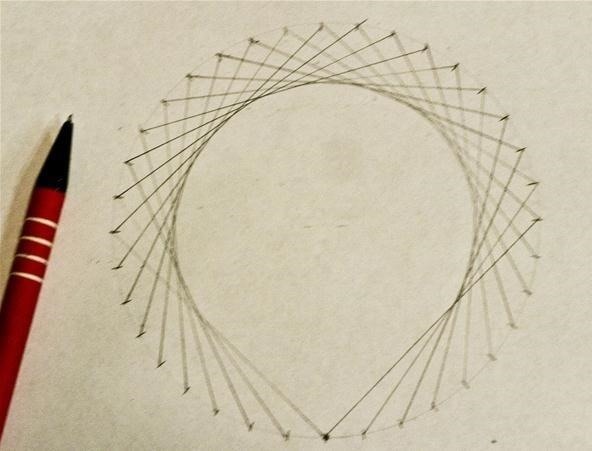
The resultant polygon has the same number of sides as there were marks on the original circle:

Geometric design featuring a circle surrounded by intersecting lines and points.

Cory Poole/WonderHowTo

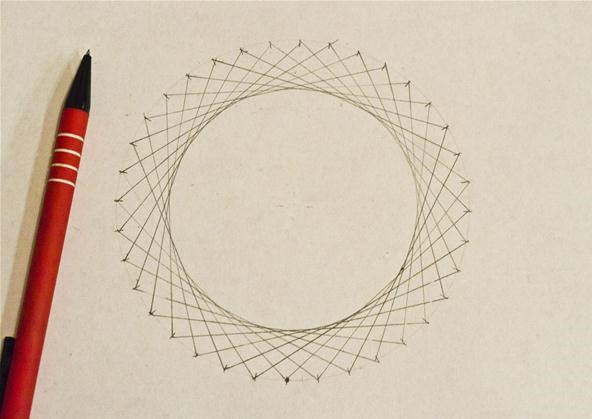
You can then use the inside circle as a starting point for creating another circle:

Geometric drawing with circular patterns and a red pen.

Cory Poole/WonderHowTo

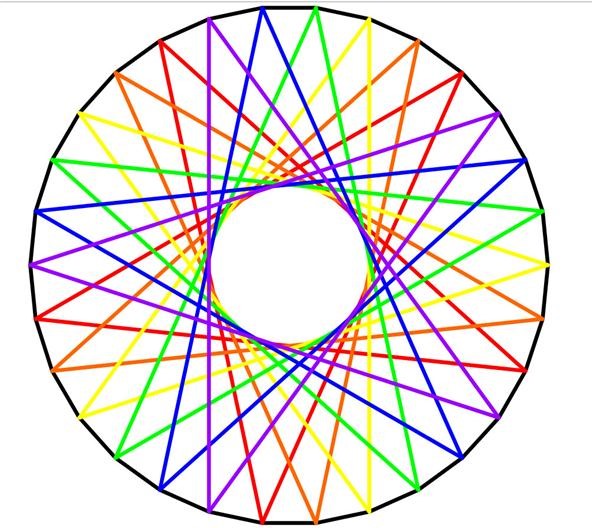
These concentric circle designs are really creating star polygons, as discussed in the posts on creating star designs on pumpkins and creating torus knots. In the image below, using GeoGebra (Classic), I took a circle with 30 marks and connected them in a design with six pentagrams. This works because 30 / 5 = 6:

Geometric pattern with multiple intersecting colored lines forming a circular design.

Cory Poole/WonderHowTo

Colorful geometric star pattern with a circular design.

Cory Poole/WonderHowTo

Option 2. Making Ellipses

Like the Earth's orbit around the Sun, an ellipse is a "closed curved shape that is flat" and best described as an oval. This squashed circle has two focal points, where "the sum of the distances to the foci is constant for every point on the curve."

Mark Off a Circle by Degrees

There are lots of ways to create ellipses, but this one is pretty fun. Start with a circle with a number of evenly spaced marks; I again chose 10 degrees. I then connected two of the marks that were 180 degrees apart, halving the circle. This line will become the major axis:

Circular diagram with numbered marks around the perimeter.

Cory Poole/WonderHowTo

Choose a Point on the Major Axis

Mark a point on your major axis. Making this point further from the center of the circle makes the ellipse longer and narrower.

Circle with numbered degrees marked around the edge.

Cory Poole/WonderHowTo

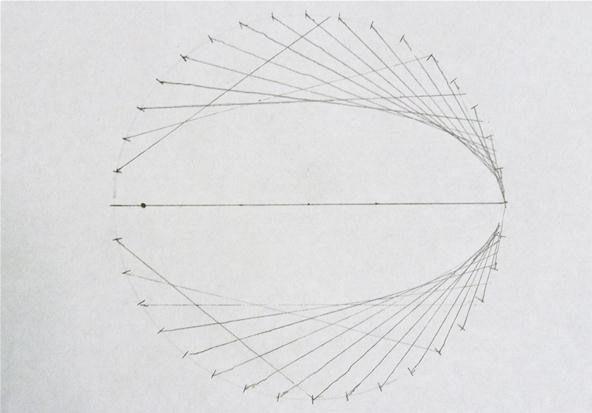
Draw a Line from the Focal Point

Make a right angle on one of the marks on the circle so that one of the sides of the angle goes through the focus. Connect the line from the mark to where it intersects the circle. Continue this process for all of the marks on the circle:

Diagonal line and arc drawn on a blank sheet of paper.

Cory Poole/WonderHowTo

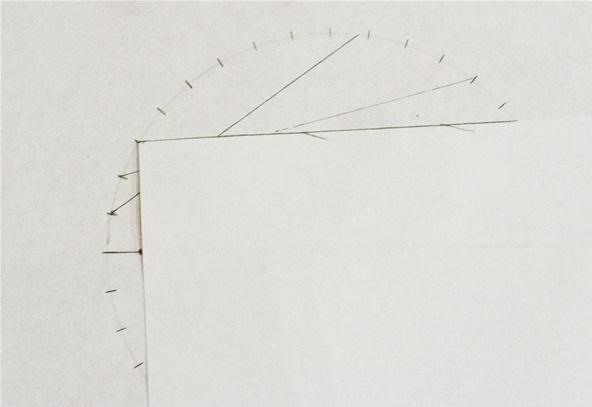
How to Create Concentric Circles, Ellipses, Cardioids & More Using Straight Lines & Circles

Cory Poole/WonderHowTo

Halfway done; the resolution increases as it gets further from the focus:

Geometrical diagram illustrating the concept of angles in a circle.

Cory Poole/WonderHowTo

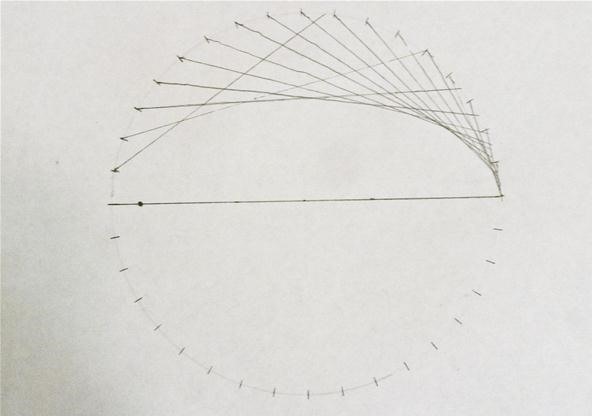
And here is the completed ellipse. Note you could improve the resolution near the focus by repeating the process using the focus on the other side:

Diagram of a parabolic curve with directional arrows indicating the focus and geometry.

Cory Poole/WonderHowTo

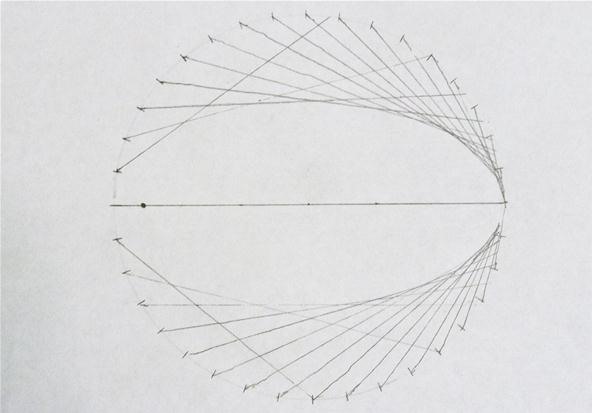
From the ellipse, I went a step further and intersected two ellipses at right angles. The result was the following heart shape, a design that brought me to mind the curve in mathematics that is known for its heart-like shape, the cardioid, which will cover next.

Geometric design featuring multiple intersecting lines within a circle.

Cory Poole/WonderHowTo

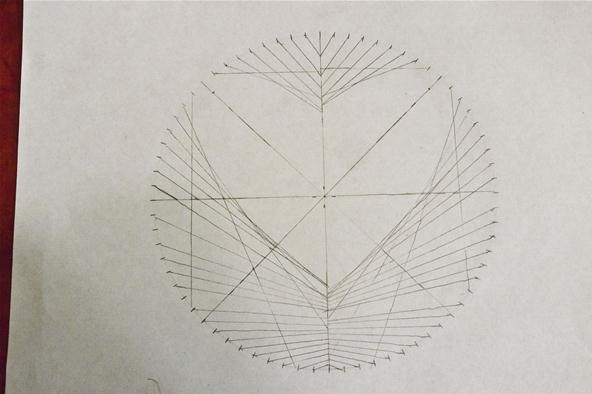
Option 3. Making Cardioids

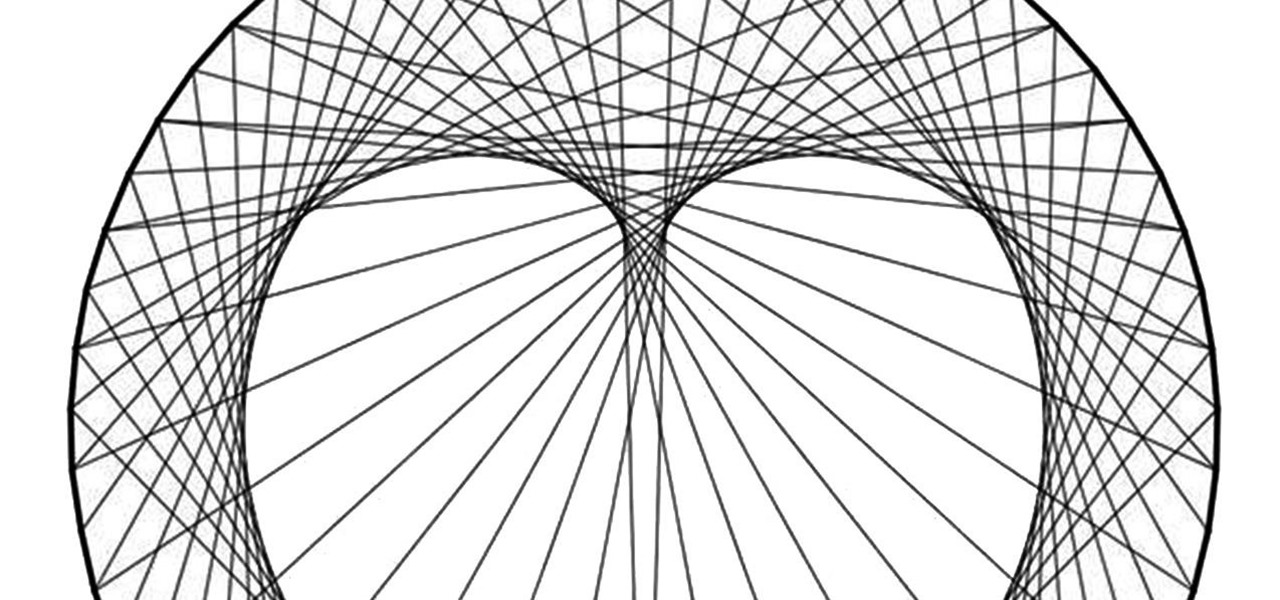
A cardioid is formed by a rolling circle's path across the circumference of another circle, all the while keeping its radius the same. The term, first used in 1741 by Giovanni de Castillon (in Philosophical Transactions of the Royal Society, 1741), originates from the Greek word for "heart." An everyday object that holds a true cardioid shape? An apple.

Mark a Circle's Circumference Evenly

To create a cardioid, start with a circle with a number of evenly spaced marks; I chose every 10 degrees on this one yet again:

Circle template with a red and black marker.

Cory Poole/WonderHowTo

Skip Ahead by Two Marks

Starting with any one mark, connect a line from it to a mark that is two marks away:

Cory Poole/WonderHowTo

Count by Ones & Twos

Take the next mark after your starting point and connect it to the mark that is two beyond the ending point of the last mark.

Take the next mark after your starting point and connect it to the mark that is two beyond the ending point of the last mark. Repeat. You are basically counting by ones on the starting points, and by twos on the ending points. Keep going and you'll begin to see the curve take shape:

Diagram of a circle with numerical markings and a curved line.

Cory Poole/WonderHowTo

Cory Poole/WonderHowTo

Geometric diagram of a circle with radius lines drawn at various angles.

Cory Poole/WonderHowTo

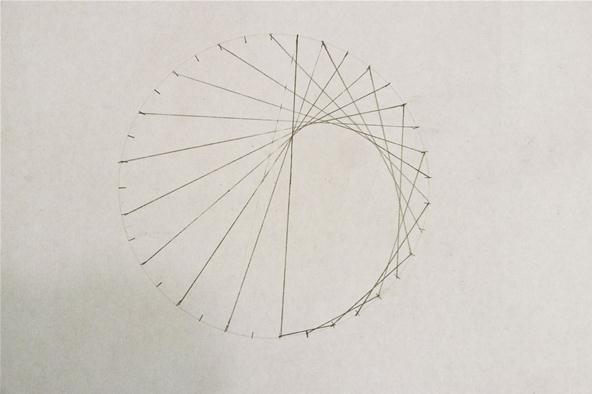
Continue on Other Side

To avoid confusion, simply focus on the mark you're working on: counting by ones for the starting point and by twos for the ending point:

Geometric illustration of a circular pattern with radiating lines.

Cory Poole/WonderHowTo

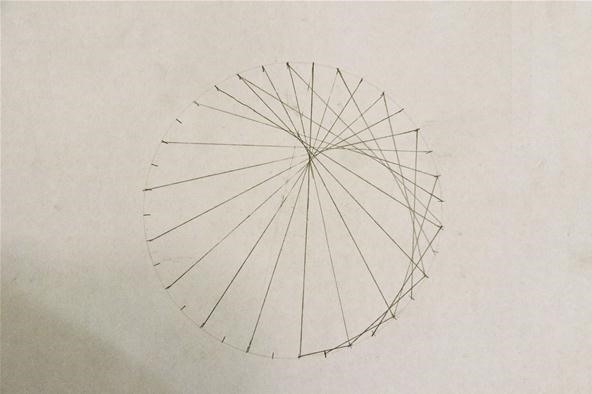
End at Original Starting Point

You'll see the heart take shape once you go completely around; stop once you return to the first mark. My completed cardioid:

Geometric representation of a circle with radial lines.

Cory Poole/WonderHowTo

You can follow this same process only by counting by threes on the ending marks or fours and you will get more sharp points. If you skip less often, you will get a more gradual spiral. The curve below was generated by counting by twos only every 4th time.

Geometric spiral illustration with intersecting lines.

Cory Poole/WonderHowTo

Colorful spiral pattern with intersecting lines.

Cory Poole/WonderHowTo

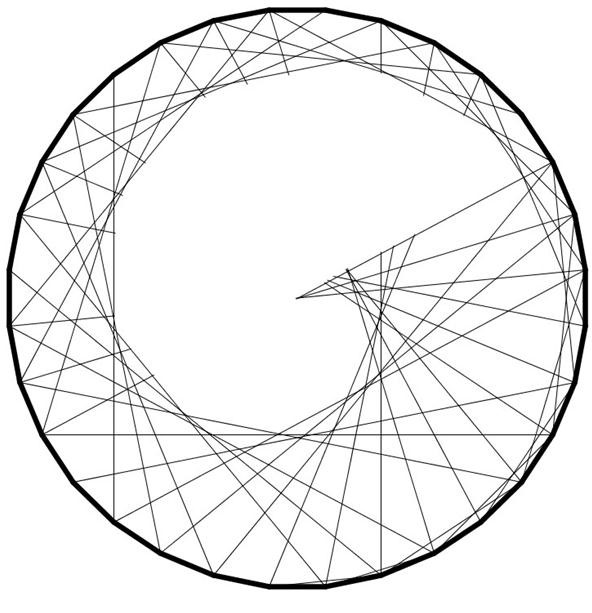
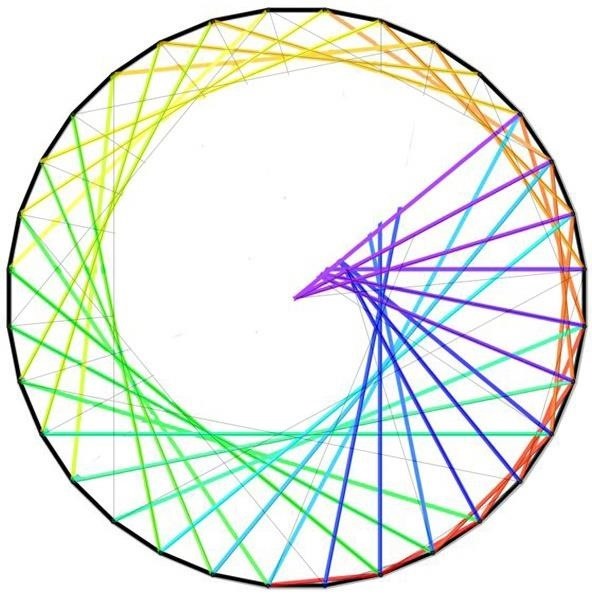
Option 4. Combine Curves & Create a Heart

Inspired, I decided to try and design a curve that looks more like a heart by combining linear sections, concentric circle sections, and cardioid sections. I think the final design looks pretty good. What do you think?

Mark a Circle into Fours

To start, you again mark a circle evenly. I chose once more 36 marks. I also made the marks at 90 degree intervals more visible; these will be important markers:

Drawing tools and a blank circular template on paper.

Cory Poole/WonderHowTo

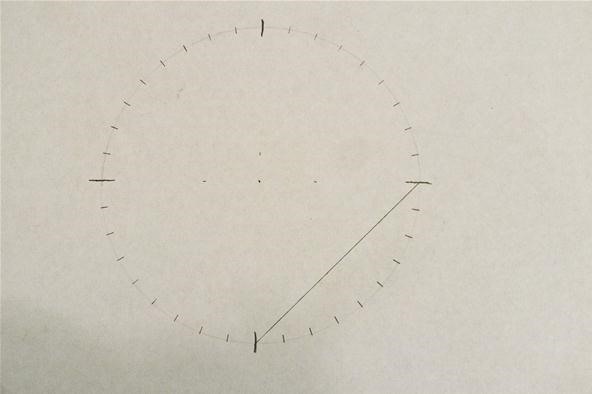
Form the Heart's Point

From the bottom, draw a line between two of the marks at 90-degree intervals. This will become part of the pointy end of the heart:

Clock face with no numbers, showing the time approximately 10:10.

Cory Poole/WonderHowTo

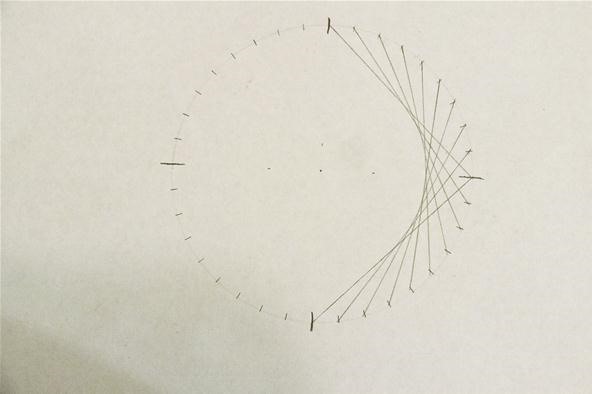
Draw Lines for a Concentric Circle

Connect the next marks as if you were making the concentric circle design. Stop when you get to the line that connects to the point 180 degrees from the starting point. You could do the same on the other side. You might not want to do this until you are completely done.

A diagram of a circular graph with lines extending from the center.

Cory Poole/WonderHowTo

Diagram of light rays demonstrating reflection in a concave mirror.

Cory Poole/WonderHowTo

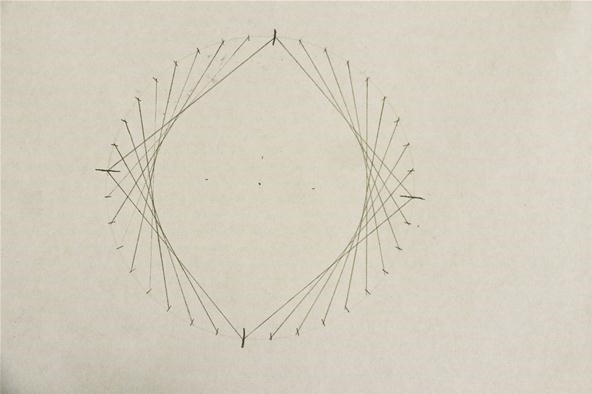
Repeat Process on Other Side

Though we go ahead and complete the concentric-circle design for the opposite side, you can choose to wait until you are completely done with one half in order to keep all the lines/marks straight:

Geometric illustration of intersecting lines forming a diamond shape.

Cory Poole/WonderHowTo

Add a Cardioid Section

Next, you will add a cardioid section, starting at the 90-degree mark right of the heart's "point." From here, connect marks by counting by ones for the starting point of the lines, and by counting by twos for the ending points:

Geometric star shape formed by intersecting lines.

Keep going: When you reach the halfway point you should have a line that connects marks that are 180 degrees apart.

Geometric pattern resembling a heart shape formed by intersecting lines.

Cory Poole/WonderHowTo

Keep going: When you reach the halfway point you should have a line that connects marks that are 180 degrees apart.

Cory Poole/WonderHowTo

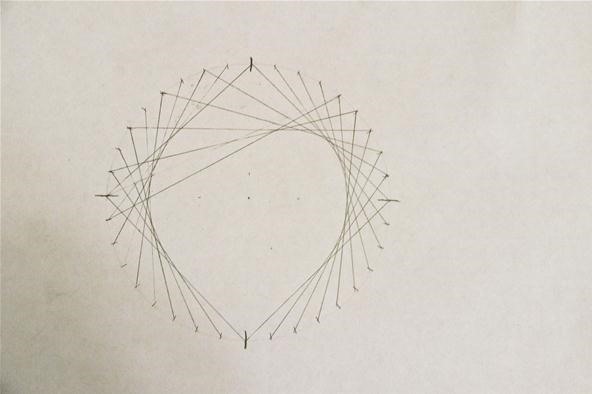
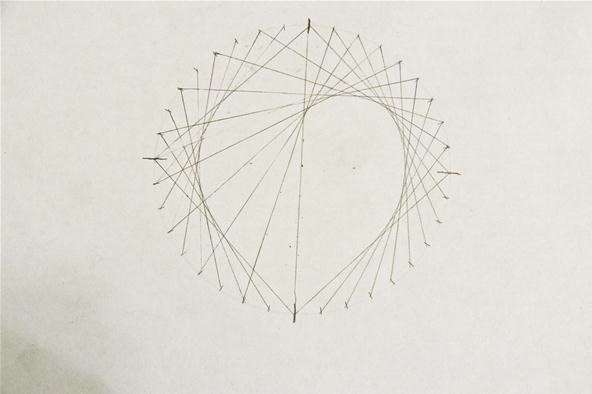
Repeat on Other Side

With the cardioid section applied to only half of the circle, you can already see the heart forming. To finish the "kardioedides," simply repeat the steps for the left side, and your heart is complete!

Heart-shaped geometric pattern created with lines and points.

Cory Poole/WonderHowTo

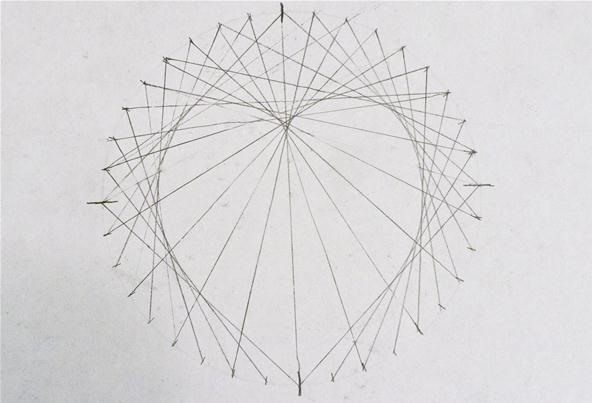
Cool, right? Finally, from this exercise, I took on one more challenge: Using a computer program, I attempted to create the same heart design using 59 marks instead of 36. I then colored it in:

Geometric heart design with interweaving lines.

Looking a bit like op art.

Abstract geometric design featuring a pink heart shape surrounded by black and white checkered patterns and rays.

Cory Poole/WonderHowTo

Looking a bit like op art.

Cory Poole/WonderHowTo

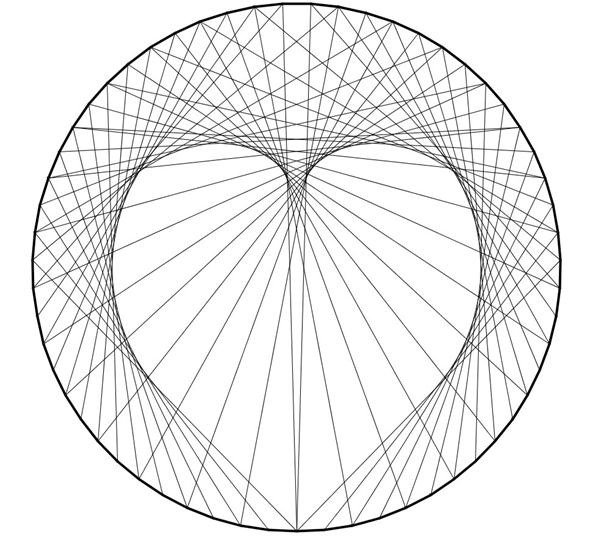
The ideas are pretty fluid when it comes to curves. Now that you're familiar with the basic mathematical curves of the concentric circle, ellipse, and cardioid, you, too, can try your own design ideas. As we've found, with a simple circle and straight lines (and some math logic), you can create any number of geometric shapes and combinations. What does your eye see?

Follow WonderHowTo on Facebook, Twitter, Pinterest, and Google+

The next big software update for iPhone is coming sometime in April and will include a Food section in Apple News+, an easy-to-miss new Ambient Music app, Priority Notifications thanks to Apple Intelligence, and updates to apps like Mail, Photos, Podcasts, and Safari. See what else is coming to your iPhone with the iOS 18.4 update.