Hot Math Craft Posts


How To: Fold a Pentakis Dodecahedron
Math Craft admin Cory Poole provided quite a few recipes for sonobe models in his blog, and I followed one to make the pentakis dodecahedron here.
How To: Create Concentric Circles, Ellipses, Cardioids & More Using Straight Lines & Circles
Using only a circle and straight lines, it's possible to create various aesthetic curves that combine both art and mathematics. The geometry behind the concentric circle, ellipse, and cardioid dates back centuries and is easily found in the world around us. From an archery target to an apple, can you name these geometric shapes?

Holiday Project: Origami Christmas Trees
Thanksgiving. It's sadly over. But happily replaced by the Christmas season!

Math Craft Monday: Community Submissions (Plus How to Make an Orderly Tangle of Triangles)
It's Monday, which means once again, it's time to highlight some of the recent community submissions posted to the Math Craft corkboard. I also thought that we'd try and create something known as an "Orderly Tangle" or "Polylink".

How To: Make the Platonic Solids Out of Playing Cards
Computer Science Professor Francesco De Comité has a fantastic gallery of mathematical images on Flickr. As part of this collection, he has a few hundred images of real or rendered polyhedra made out of paper or playing cards which he calls "slide togethers." These are constructed by making cuts and then sliding one component into the other, creating a shape without using any glue. He constructed the entire set of the platonic solids—the cards form their edges—which can be seen in the image b...

Math Craft Monday: Community Submissions (Plus How to Make a Modular Origami Intersecting Triangles Sculpture)
It's once again Monday, which means it's time to highlight some of the most recent community submissions posted to the Math Craft corkboard. I also thought we'd take a look at building a model that has appeared in numerous posts. It's the simplest of the intersecting plane modular origami sculptures: The WXYZ Intersecting Planes model.

How To: Make Icosahedral Planet Ornaments
In honor of the new Astronomy World, I thought we should look at a few planetary icosahedrons. The icosahedron is the most round of the Platonic solids with twenty faces, thus has the smallest dihedral angles. This allows it to unfold into a flat map with a reasonably acceptable amount of distortion. In fact, Buckminster Fuller tried to popularize the polyhedral globe/map concept with his Dymaxion Map.

News: Origami Sierpinski Tetrahedron Constructed with 250+ Modules
I've already posted a brief roundup of interesting models folded by Michal Kosmulski, expert orgami-ist and IT director at NetSprint. However, I didn't include my favorite model, because I felt it deserved its own post. Kosmulski folded an elaborate and large Sierpinski tetrahedron, which he deems "level 3" in difficulty. (Translation: hard). It is constructed with 128 modules and 126 links, based on Nick Robinson's trimodule.

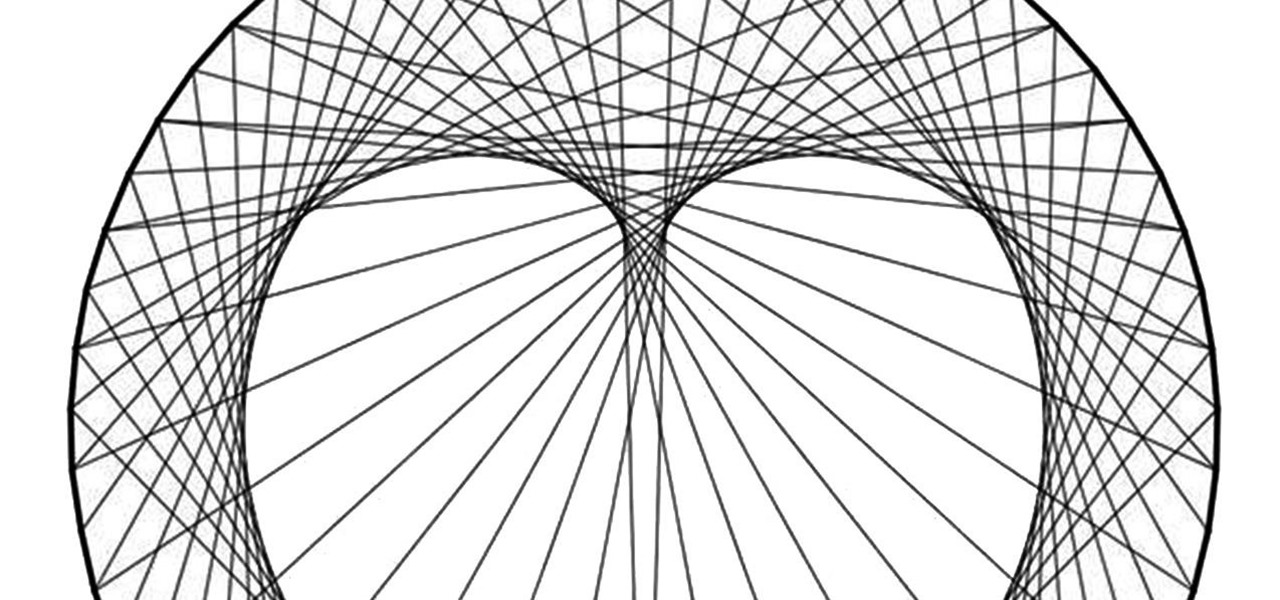
How To: Create Parabolic Curves Using Straight Lines
Curve stitching is a form of string art where smooth curves are created through the use of straight lines. It is taught in many Junior High and High School art classes. I discovered it when my math students started showing me the geometric art they had created.

Modular Origami: How to Make a Cube, Octahedron & Icosahedron from Sonobe Units
Modular origami is a technique that can be used to build some pretty interesting and impressive models of mathematical objects. In modular origami, you combine multiple units folded from single pieces of paper into more complicated forms. The Sonobe unit is a simple example unit from modular origami that is both easy to fold and compatible for constructing a large variety of models. Below are a few models that are easy to make using this unit.

Modular Origami: How to Make a Truncated Icosahedron, Pentakis Dodecahedron & More
Last post, the Sonobe unit was introduced as a way to use multiple copies of a simply folded piece of paper to make geometric objects. In this post, we are going to explore that concept further by making two more geometric models. The first is the truncated icosahedron, which is a common stitching pattern for a soccer ball. The second was supposed to be the pentakis dodecahedron, but through systematic errors last night, I actually built a different model based off of the rhombic triacontahed...

How To: Welcome to Math Craft World! (Bonus: How to Make Your Own Paper Polyhedra)
Welcome to Math Craft World! This community is dedicated to the exploration of mathematically inspired art and architecture through projects, community submissions, and inspirational posts related to the topic at hand. Every week, there will be approximately four posts according to the following schedule:

How To: Make a Hyperbolic Paraboloid Using Skewers
In Monday's post, we created a sliceform model of a hyperbolic paraboloid. In today's post, we will create a similar model using skewers. The hyperbolic paraboloid is a ruled surface, which means that you can create it using only straight lines even though it is curved. In fact, the hyperbolic paraboloid is doubly ruled and is one of only three curved surfaces than can be created using two distinct lines passing through each point. The others are the hyperboloid and the flat plane.

Math Craft Monday: Community Submissions (Plus How to Make a Sliceform Hyperbolic Paraboloid)
It's Monday, which means once again, it's time to highlight some of the most recent community submissions posted to the Math Craft corkboard. I also thought we'd take a look at building a sliceform model of a hyperbolic paraboloid.

News: Tom Friedman's Twisted Math Art
Tom Friedman is one of my favorite artists. He's got a great sense of humor, and his work is meticulous and beautiful. He forays into Math Art, and from a partisan perspective, he seems to be inspired by mathematics, but the end results are more of a whimsical twist than a mathematically "correct" execution. But I could be totally wrong. Comment below and fill me in.

News: Math Craft Inspiration of the Week: The Kinetic Wave Sculptures of Reuben Margolin
Reuben Margolin builds large scale kinetic sculptures based off of mechanical waves. Some of his sculptures contain hundreds of pulleys all working in harmony with each other to create sinusoidal waves and their resulting interference patterns. He designs them all on paper and does all of the complicated trigonometric calculations by hand. Everything is mechanical; there are no electronic controllers.

News: Sierpinski Christmas Tree
This three dimensional Sierpinski tetrahedral structure was created with a lot of help from my Year 10, 12 and 13 classes. It is inspired by the Sierpinski triangle fractal.

News: Math Craft Inspiration of the Week: The Curved Geometric Paper Sculptures of Richard Sweeney
Richard Sweeney is an incredible artist whose body of work consists mainly of sculptures made from paper. His art is often related to origami, and much of his work is related to geometrical forms. I personally really love his modular forms in paper. Many of them are based off of the platonic solids, which have been discussed in previous posts this week. Below are a small number of his sculptures, which are very geometric in nature.

News: 7 Templates for Slide-Together Geometric Paper Constructions
The "slide-together" paper construction method is a fun and satisfying way to build 3D geometric objects. It only requires paper, scissors or an exacto knife, and some patience.
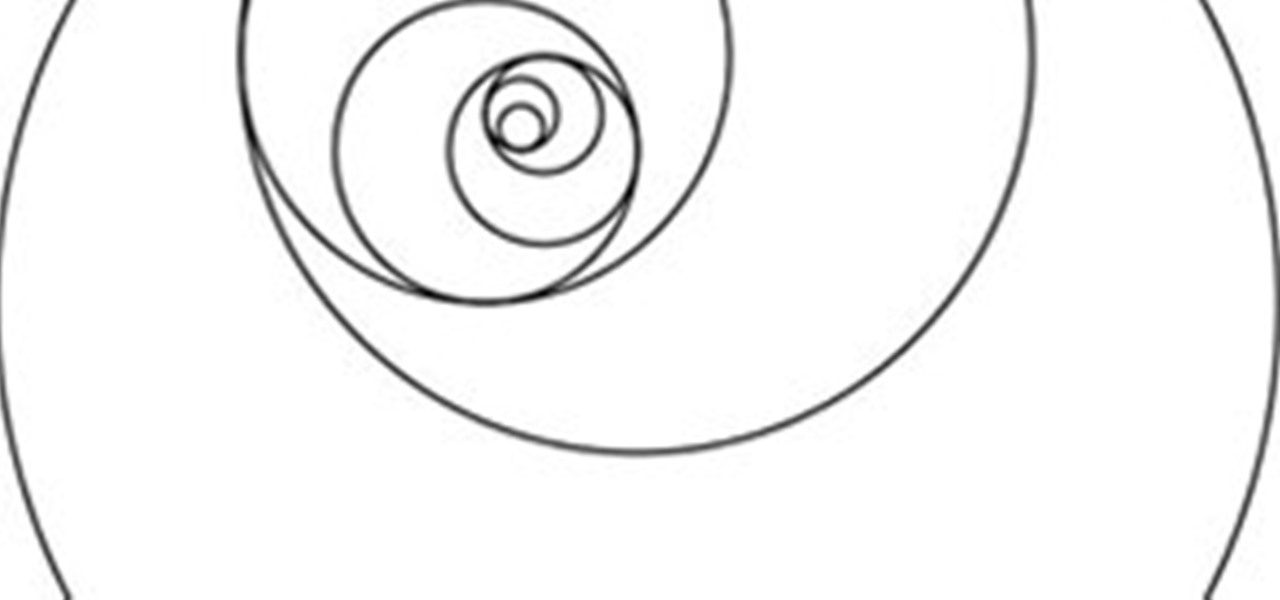
News: Making Art with the Golden Ratio
You can do some pretty cool stuff with the golden ratio. The image above is made from taking each quarter-circle in the golden spiral and expanding it into a full circle. In the second image, the spiral and the golden rectangles are overlaid on the the first image, showing how it works.
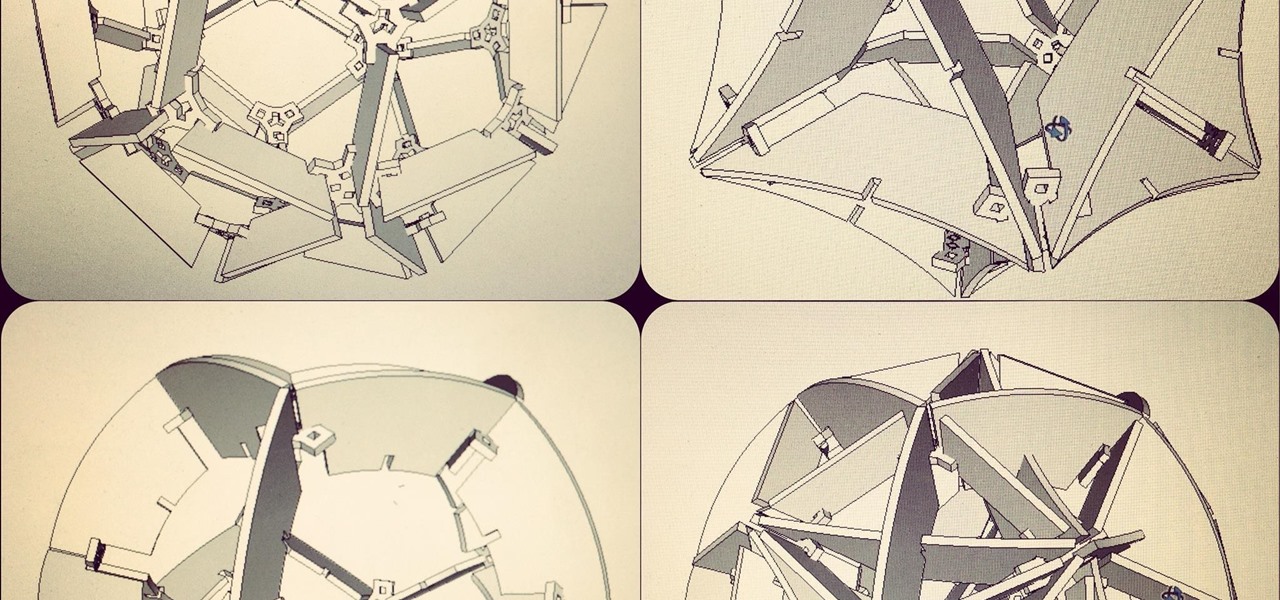
News: A 3-in-1 Model
These drawings were made with Google SketchUp. There is a dodecahedral model, icosahedral model, and a third I don't know the name of, made of rhombic faces obtained by connecting vertices of the other two. The final image is all three models together. I'll use a ShopBot CNC router to cut out the pieces this week.

How To: Holy String Art, Batman! 6 of the Coolest Thread Art Projects Ever
You may remember string art from your elementary school days. If so, it probably makes you think of the 2D geometrical designs that took every ounce of patience you had as a kid. Or those laborious curve stitch drawings, which string art was actually birthed from. But thanks to some innovative modern artists, string art has gotten a lot more interesting. Here are some of the most creative applications so far.

News: Parabolic Art in EL-Wire by Ben Yates
This is a new line of work I've started - inspired by string art of Archimedean Lines, these are 3-dimensional sculptures made using Electro-Luminescent Wire weaved around a clear acrylic frame. They hang on the wall, but each has a sense of depth so their look alters from different angles. The EL-Wire is a copper wire coated with a phosphor so it glows its entire length, and then coated with a plastic sleeve so that it can be handled and bend around any shape.

How To: Design Your Own Playing Card Sculpture
Download the Software Go to the Antiprism downloads page. Download and install Antiprism 0.20.

News: Mathematical Quilting
I got hooked on origami sometime after Math Craft admin Cory Poole posted instructions for creating modular origami, but I had to take a break to finish a quilt I've been working on for a while now. It's my first quilt, and very simple in its construction (straight up squares, that's about it), but it got me thinking about the simple geometry and how far you could take the design to reflect complex geometries. Below are a few cool examples I found online.

News: Palm-Sized Pentakis Dodecahedron
I finally got around to making the pentakis dodecahedron from the instructions in Math Craft admin Cory Poole's blog post. It's not tightened/straightened up yet because I just noticed that I have two black and white and two blue and green compound modules next to each other (but no purple and pink modules next to each other—to the math experts, this is a parity thing, as you can only have even numbers of modules paired up next to each other).

Mathematical Holiday Ornaments: Escher "Snow Flakes"
This week's post on creating 6-sided Kirigami Snowflakes got me interested in seeing whether I could use the process to create tessellation snowflakes using the method. I still haven't succeeded, but I did decide to make some ornaments based off a few of the tessellations by M.C. Escher that have a 6 sided symmetry.

Modular Origami: Icosahedron, Octahedron & Cube
I spent the holiday weekend becoming fluent in the basics of modular origami. With practice, you can churn out the below models surprisingly quickly.

News: 30 Square Sliding Modular Origami
Cory's post with instructions and templates Here's my first attempt at the 30 squares model. I needed to be a little bit more careful in the measuring and cutting as not everything matches up - but it is still a really pleasing shape.

News: Folding Everlasting Gobstoppers
I came across this Dutch site called "Wat Maakt Suzette Nu?", which featured a project created with Math Craft instructions for modular origami. Suzette, the creator, did an incredible job in terms of craftsmanship and color...

Math Craft Monday: Community Submissions (Plus How to Make a Magic Square Tetraflexagon)
It's Monday, which means once again, it's time to highlight some of the recent community submissions posted to the Math Craft corkboard. In this post, we'll also make a flexagon, which is a type of transformable object.

News: Math Craft Inspiration of the Week: The Origami Tessellations of Eric Gjerde
Eric Gjerde is a master of origami who devotes much of his energy on origami tessellations. Some of his pieces fold nearly flat, forming layers that add just a hint of depth. These pieces look beautiful when lit from behind, due to the variations in brightness and color. Other pieces utilize three dimensions more fully, with repeated structures rising out of the flat page.

How To: Make Knot Sculptures from Soft Metals
In mathematics, a knot is a closed circle in a three-dimensional space that crosses itself multiple times. Since it is closed, it has no ends to tie, meaning you can't actually create such a knot. However, if you tie the ends together after you create a knot in the standard way, you will have something that is close to the mathematical description. In this post, we will explore the creation of mathematical knot sculputures using copper tubing and solid solder wire.


News: Curvy origami designs I am working on:
I have a lot more images at hyperqbert's Profile • Instagram.

News: Origami Valentine's Day Present
I made a Origami Valentine's day present for my Little Sister and Neice using heart and rose origami patterns I found on-line and put them in a backet with heart shaped lollipop I bought from Target.

How To: Make a 'Flex Mex'—A Mathematically Delicious Hexaflexagon Burrito
Here's a great excuse to play with your food—and learn some math while you're at it. We've all seen a hexaflexagon folded out of paper, but how about a burrito? Vi Hart, a "mathmusician" over at the Khan Academy, came up with the Flex Mex, a burrito folded into a hexaflexagon with all the toppings inside. The spreadable ingredients (guacamole, sour cream and salsa) go inside the folds, then it's topped with beans and cheese.

News: Sonobe modular Fun
Made some Sonobe modules with some note cards. I made a big one with poster paper...Paper magic


News: The Incredible Polyhedra Models of Mario Marín
Mario Marín has made an incredible collection of models and sculptures based on polyhedra, often using everyday and readily available items. The site is in Spanish, but click on the links on the left and there are plenty of photographs, and more can be seen in Mario's blog.


