Math Craft Features


News: Polyhedron Animation
Below, polyhedron animation test #1. The model was folded using Cory Poole's modular origami tutorial.

Math Craft Monday: Community Submissions (Plus How to Make Mobius Strips)
It's another Monday, which means once again, it's time to highlight some of the recent community submissions posted to the Math Craft corkboard. Additionally, I thought we'd take a look at the Mobius Strip.

Holiday Project: Origami Christmas Trees
Thanksgiving. It's sadly over. But happily replaced by the Christmas season!

How To: Make a Sonobe Jasmine Dodecahedron
Math Craft admin Cory Poole posted instructions on How to Make a Cube, Octahedron & Icosahedron from Sonobe Units, plus some great complex models in his article, How to Make a Truncated Icosahedron, Pentakis Dodecahedron & More. These models use the standard sonobe unit and a coloured variant.

News: DIY Papercraft Architecture with Lighting
This is probably the least "Mathy" thing I will ever post. In my opinion, it's impossible to have architecture that isn't mathematical in some sense, so I am posting it anyway. Two years ago, I made a papercraft version of a cathedral in Christchurch New Zealand (It was severely damaged in an earthquake earlier this year) and cut holes for all of the windows and lit it with LED lights. I gave it to my Mom as a Christmas gift. I thought it made for a pretty amazing "Christmas Village" piece.

News: Folding Everlasting Gobstoppers
I came across this Dutch site called "Wat Maakt Suzette Nu?", which featured a project created with Math Craft instructions for modular origami. Suzette, the creator, did an incredible job in terms of craftsmanship and color...

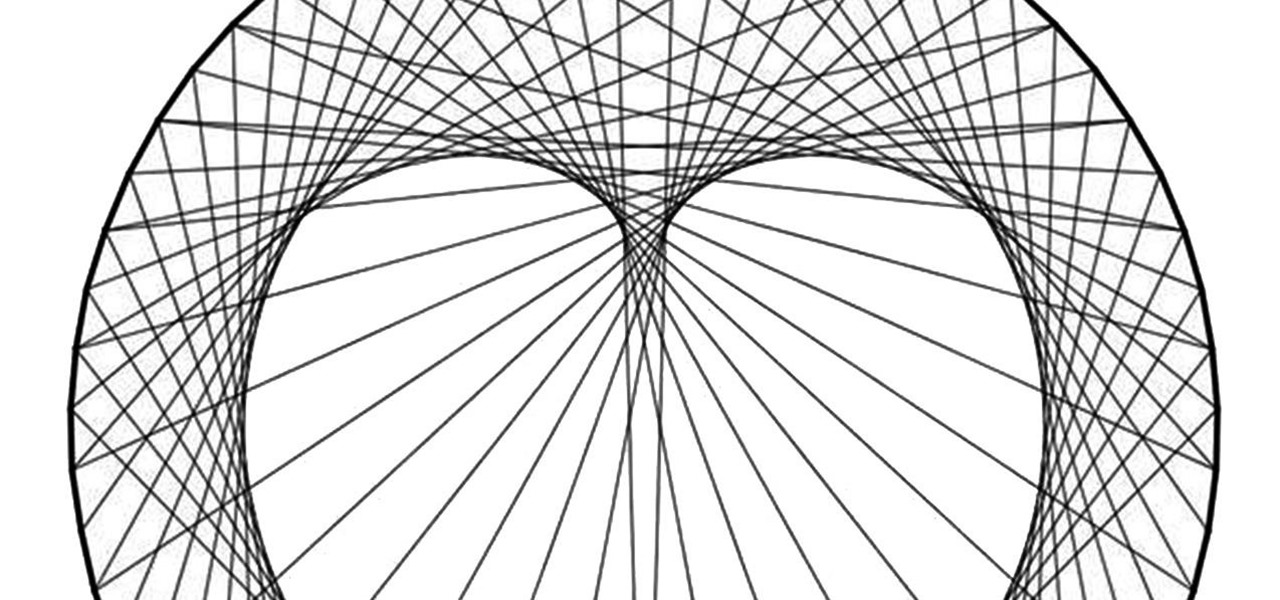
How To: Holy String Art, Batman! 6 of the Coolest Thread Art Projects Ever
You may remember string art from your elementary school days. If so, it probably makes you think of the 2D geometrical designs that took every ounce of patience you had as a kid. Or those laborious curve stitch drawings, which string art was actually birthed from. But thanks to some innovative modern artists, string art has gotten a lot more interesting. Here are some of the most creative applications so far.

How To: Make Yin-Yang Pillow Boxes
Here's a Math Craft project that takes less than 20 minutes, has an attractive, practical result, and is at least a little mind-blowing due to folding along curves.

News: Best Math Class Project Ever
I wish there was more information about this impressively massive sonobe model, but all I can glean is that it appears to have been made by Imogen Warren, and was posted by Room 3. So awesome.

How To: Make Nested Cube and Octahedron Boxes
These boxes are inspired by a comment from Imaatfal Avidya on a corkboard post on Platonic polyhedra from sonobe units. Imaatfal was commenting about how the cube and octahedron are related to each other.

Math Craft Monday: Community Submissions (Plus Polyhedral Stellation)
It's another Monday, which means it's once again time to highlight some of the recent community submissions posted to the Math Craft corkboard. Additionally, I thought we'd take a look at the process of stellation and make some stellated polyhedra out of paper.Rachel Mansur of Giveaway Tuesdays posted a video from animator Cyriak Harris, which zooms into fractal hands, where each fingertip also has a hand and fingers. A few more details can be found here, as well as some other really cool pic...

News: 180 Unit Sonobe Buckyball
I wondered how silly you could get with sonobe, and had a bash at a buckyball, which is a fullerene (technically a truncated isocahedron; you can see a simple model here). It's twelve pentagons—each surrounded by 5 hexagons (20 in total)—making a football shape in England or a soccer ball shape in the USA.

How To: Carve Polyhedral Pumpkins
Halloween is coming up, so many of you may have a need or desire to carve a pumpkin and turn it into a Jack O' Lantern. This week we are going to explore carving our pumpkins into interesting geometric shapes. In this post, we will carve the pumpkins into spherical versions of polyhedra, and in Thursday's post we will carve 2 dimensional stars and some simple fractal designs into the pumpkins.

How To: Make Torus Knots from Soft Metals
Torus knots are beautiful knots formed by wrapping a line around a torus and tying the ends together to form a loop. The resulting knot has a star-like appearance when viewed from above. The 36 examples with the least number of crossings can be seen at the Knot Atlas's page on torus knots.

News: Modular Paper Sculptures Based off of Richard Sweeney's Work
Here's my version of his icosahedron: I colored it in this one so that you can see the pentagonal faces of a dodecahedron:

Mathematical Holiday Ornaments: Escher "Snow Flakes"
This week's post on creating 6-sided Kirigami Snowflakes got me interested in seeing whether I could use the process to create tessellation snowflakes using the method. I still haven't succeeded, but I did decide to make some ornaments based off a few of the tessellations by M.C. Escher that have a 6 sided symmetry.

News: Math Craft Inspiration of the Week: The Mathematical Lego Sculptures of Andrew Lipson
Andrew Lipson builds sculptures based off of Mathematical objects using standard Lego bricks. He has built models of knots, Mobius strips, Klein bottles, Tori, Hoberman spheres (using Lego technic pieces), and recreations of M.C. Escher works.

News: Math Craft Inspiration of the Week: The Polyhedral Metal Sculptures of Vladimir Bulatov
Vladimir Bulatov makes sculptures of fantastic variations on polyhedra and other geometric objects. His site is full of incredible metal, glass, and wooden geometric sculptures, including a full section on pendants and bracelets. Here are just a dozen or so of the hundreds of beautiful objects that he has produced.

News: The Incredible Polyhedra Models of Mario Marín
Mario Marín has made an incredible collection of models and sculptures based on polyhedra, often using everyday and readily available items. The site is in Spanish, but click on the links on the left and there are plenty of photographs, and more can be seen in Mario's blog.

Math Craft Monday: Community Submissions (Plus How to Make a Magic Square Tetraflexagon)
It's Monday, which means once again, it's time to highlight some of the recent community submissions posted to the Math Craft corkboard. In this post, we'll also make a flexagon, which is a type of transformable object.

News: Alexander Graham Bell's Tetrahedral Obsession
Oobject put together a neat compilation of the famous telephone inventor's love for tetrahedrons. Scroll down to see his collection of pyramids, building towers, buildings, boats, kites and planes—all made completely out of tiny tetrahedrons. Amazing.

News: TUVWXYZ Star Model
So beautiful... I'm looking forward to tackling this one: Via David Petty:

News: Parabolic Art in EL-Wire by Ben Yates
This is a new line of work I've started - inspired by string art of Archimedean Lines, these are 3-dimensional sculptures made using Electro-Luminescent Wire weaved around a clear acrylic frame. They hang on the wall, but each has a sense of depth so their look alters from different angles. The EL-Wire is a copper wire coated with a phosphor so it glows its entire length, and then coated with a plastic sleeve so that it can be handled and bend around any shape.

News: Orderly Tangle Earrings
I decided I would make those earrings I alluded to in Monday's Post on orderly tangles. I had to shrink the templates down so that the triangles are about 2 cm on a side. I used 110 lb cardstock and and painted them using metallic leafing paint in gold, silver, copper, and brass. I would put up a tutorial, except I think that this project would be too frustrating for most people. All I can suggest is that you make the orderly tangle of 4 triangles multiple times and just keep shrinking the si...

News: M.C. Escher Square Tessellation Ornaments
Imatfaal's awesome post on Escher's tessellations on Polyhedra reminded me of some ornaments I made this summer. I made some of Escher's square tessellations onto cubes and then reprojected them onto spheres. I actually used a 60 sided Deltoidal hexecontahedron since that net is fairly easy to fold and looks pretty round.

News: Palm-Sized Pentakis Dodecahedron
I finally got around to making the pentakis dodecahedron from the instructions in Math Craft admin Cory Poole's blog post. It's not tightened/straightened up yet because I just noticed that I have two black and white and two blue and green compound modules next to each other (but no purple and pink modules next to each other—to the math experts, this is a parity thing, as you can only have even numbers of modules paired up next to each other).

News: Sonobe modular Fun
Made some Sonobe modules with some note cards. I made a big one with poster paper...Paper magic

News: An Octahedron Made with Sonobe Units
My first attempt with the sonobe unit! I'm now addicted. I'll be spending the holiday folding. Instructions here.


News: DIY Origami Christmas Tree
This is how my version of an origami Christmas tree turned out based on the instructions I posted awhile back. Cory also made a version from white glossy paper, which looks great. I opted for the green and brown look, but it wasn't easy.

How To: Carve Fractals and Stars on Pumpkins
Fractals and stars are two of the most beautiful and complicated-looking classes of geometric objects out there. We're going to explore these objects and how to carve them on a pumpkin. Unlike the last one on carving polyhedral pumpkins, where we used the entire pumpkin to carve a 3 dimensional shape, the pumkin carving in this post will involve two-dimensional images on a small part of the pumpkin's surface.

News: DIY Crazy Paper Toy
This is just too cool. As soon as I saw this, I thought, "Math Craft!"
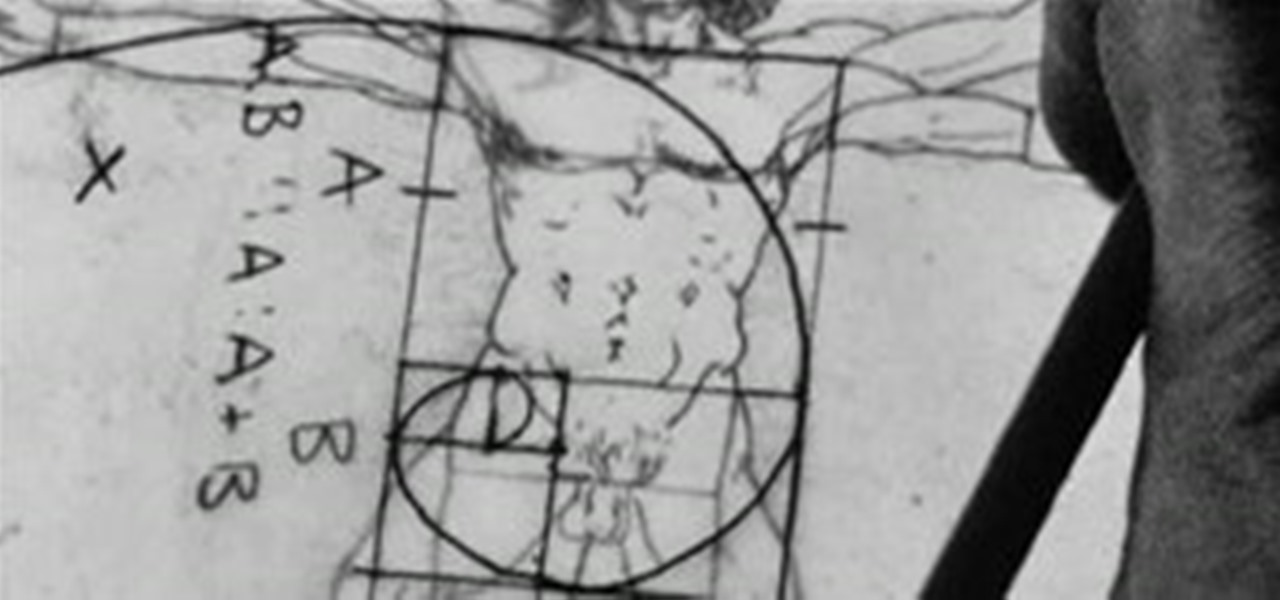
Math Craft Monday: Community Submissions (Plus How to Make the Golden Spiral)
It's Monday, time to highlight some of the community submissions posted to the Math Craft corkboard. One of these posts inspired me so much, I think it merits a closer look. Today, I present a "simple" method for making a golden spiral using just a straight edge, a compass, and a template, inspired by RJ Ellicock's golden ratio post.

News: Math Craft Inspiration of the Week: Electrically Generated Fractal Branching Patterns
Natural processes often create objects that have a fractal quality. Fractal branching patterns occur in plants, blood vessel networks, rivers, fault lines, and in several electrical phenomena. Many of these processes take lifetimes, or even occur on geological timescales. But this is not the case for electrical phenomena. They often occur near instantaneously. One example would be the branching patterns that sometimes occur in lightning.

News: Math Craft Inspiration of the Week: Marble Binary Calculators & Other Mechanical Computers
Since today (11/11/11) is the last 6 digit binary date this century, I thought we should look at some kinetic binary calculators.

How To: Make Yin-Yang Modular Polyhedra
Last Thursday's post demonstrated how to Make Yin-Yang Pillow boxes, which were based on equilateral triangles and squares. The units for making these boxes were created by Phillip Chapman-Bell, who runs an amazing origami blog and has a spectacular flickr photostream. Using these units, you can make also make 4 of the 5 platonic solids. I made an additional template based on the regular pentagon so that the dodecahedron can be built completing the set.

How To: Make Fractal Cupcakes
Last post, we looked at fractal cookies based off of the recipe by Evil Mad Scientist Laboratories. In this post, we'll follow their recipe for fractal cupcakes based off of the Koch Snowflake, which we used previously to decorate pumpkins for Halloween.

News: Math Craft Inspiration of the Week: The Intricate Sonobe Art of Meenakshi Mukerji
Last week Math Craft admin Cory Poole demonstrated how to make three of the platonic solids from Sonobe units: the cube, the octahedron, and the icosohedron; but where was the dodecahedron? I was pushed to find out how to make a sonobe dodecahedron from this beautiful picture (below) that Rachel Mansur posted on the corkboard.

Math Craft Monday: Community Submissions (Plus Tiling with Coins)
It's Monday, and once again it's time to highlight some of the community submissions posted to the Math Craft corkboard. In addition, I thought we'd take a look at having fun with the geometrical properties of polygons and circles by using one of the best circles I know, the penny.

News: Platonic Solid Made from Rider Back Playing Cards
Below, my construction of a Platonic Solid made from playing cards. To make your own, templates can be found at George Hart's site; there are also full step-by-step instructions here.