The Latest on Math Craft












news
A 3-in-1 Model 












Featured On WonderHowTo:
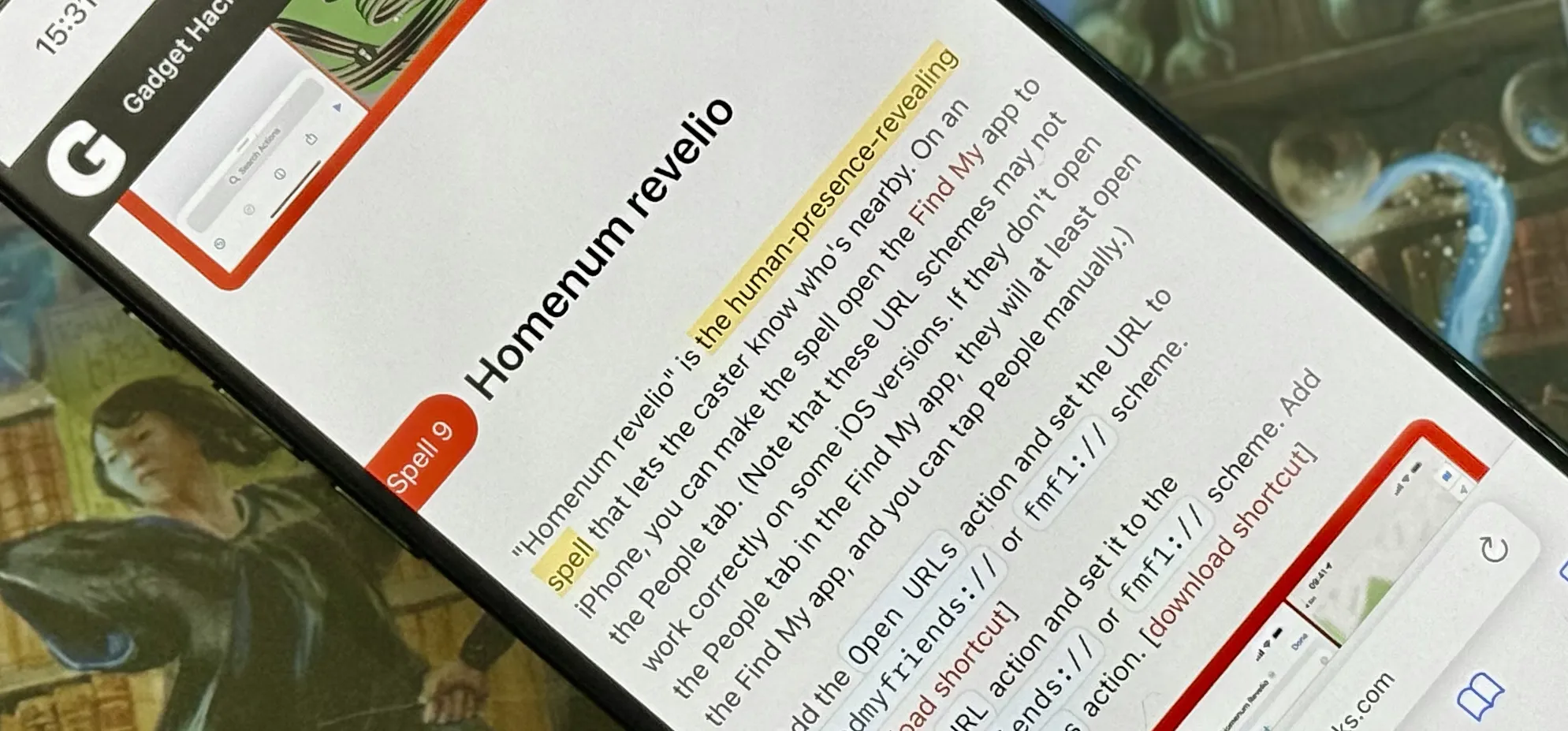
Productivity & Shortcuts






Featured On WonderHowTo:
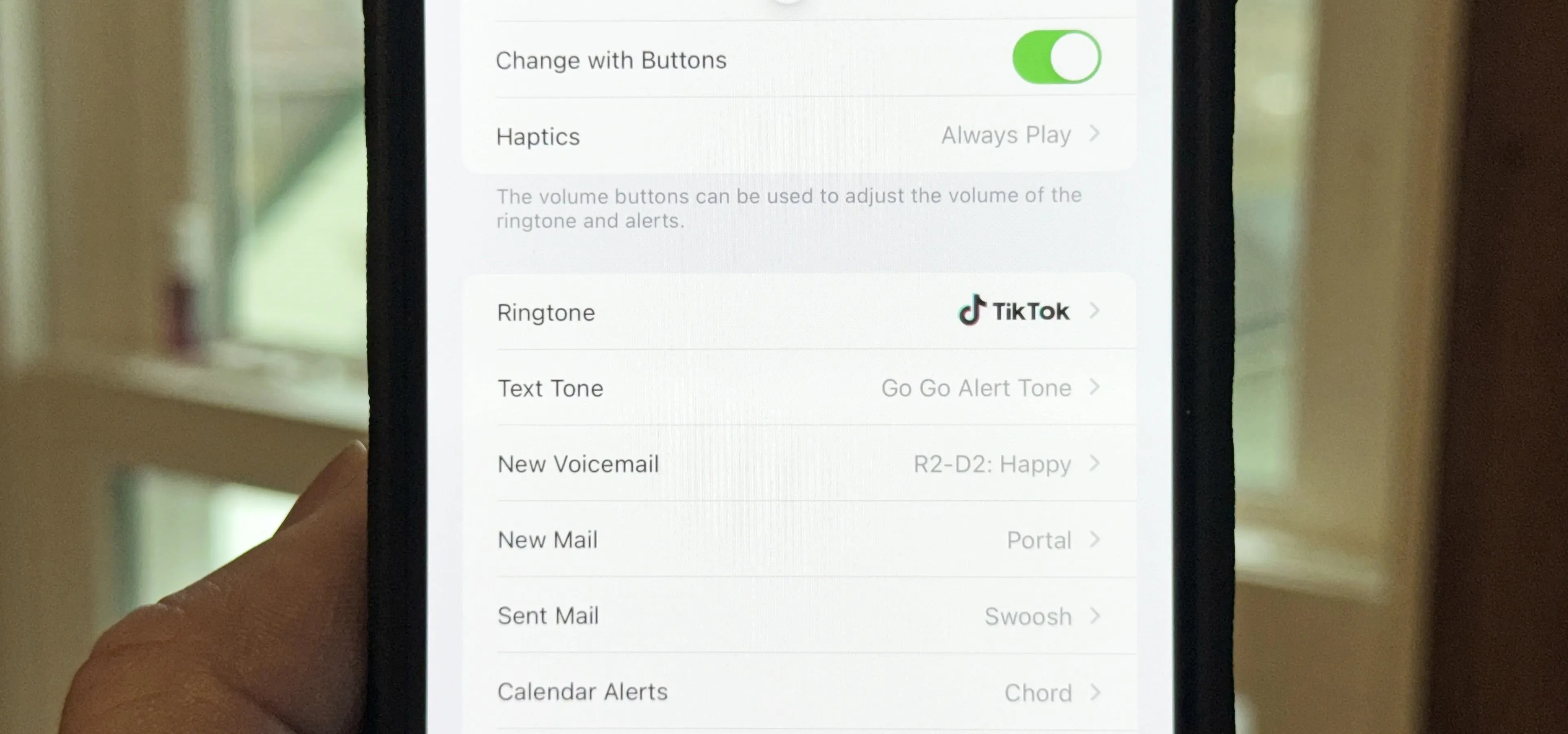
Music & Audio






Featured On WonderHowTo:
Augmented Reality







Featured On WonderHowTo:
Gaming