forum
My Hobby 








news
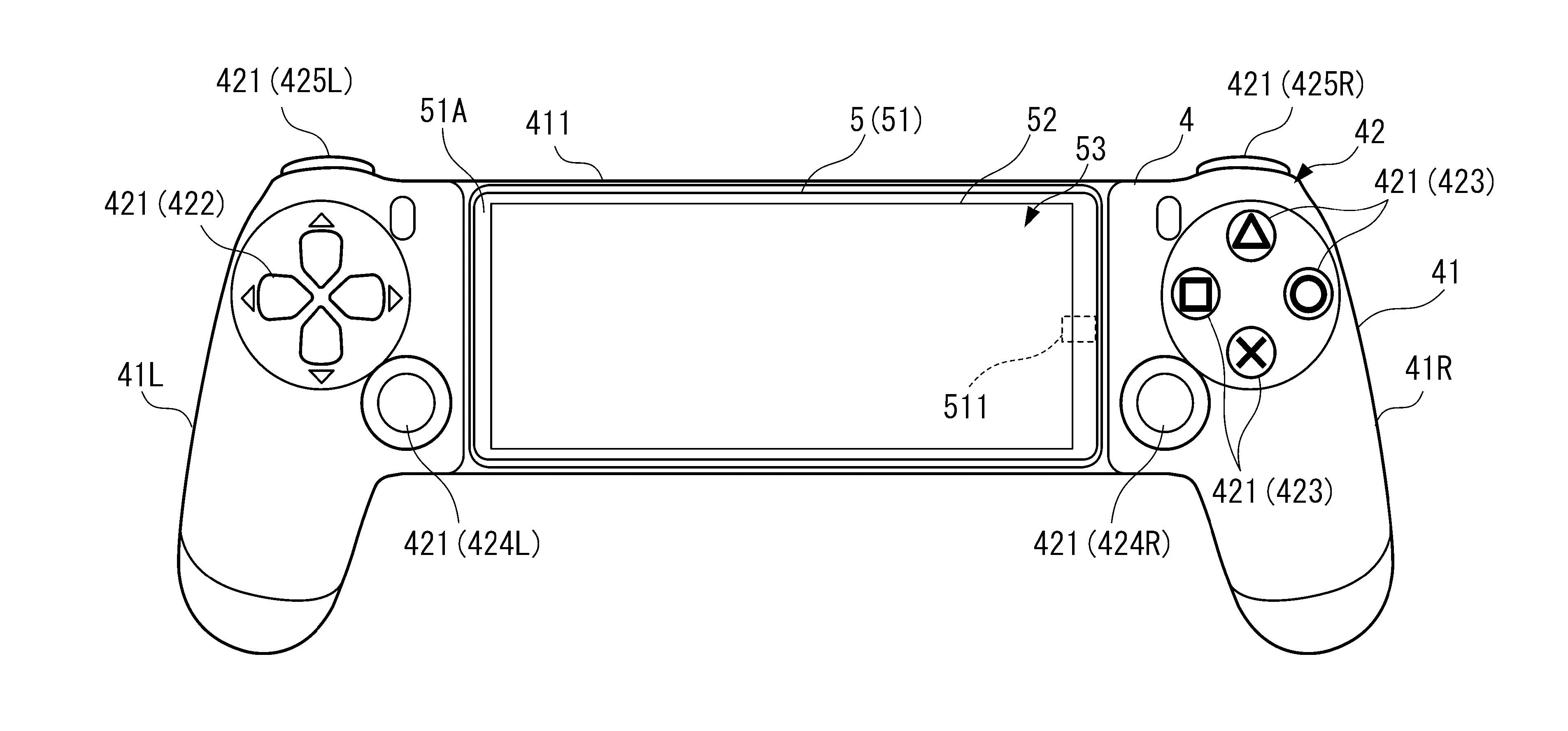
A 3-in-1 Model 












Featured On WonderHowTo:
Productivity & Shortcuts






Featured On WonderHowTo:
Music & Audio






Featured On WonderHowTo:
Augmented Reality







Featured On WonderHowTo:
Gaming