News and Updates about Math Craft






















Featured On WonderHowTo:
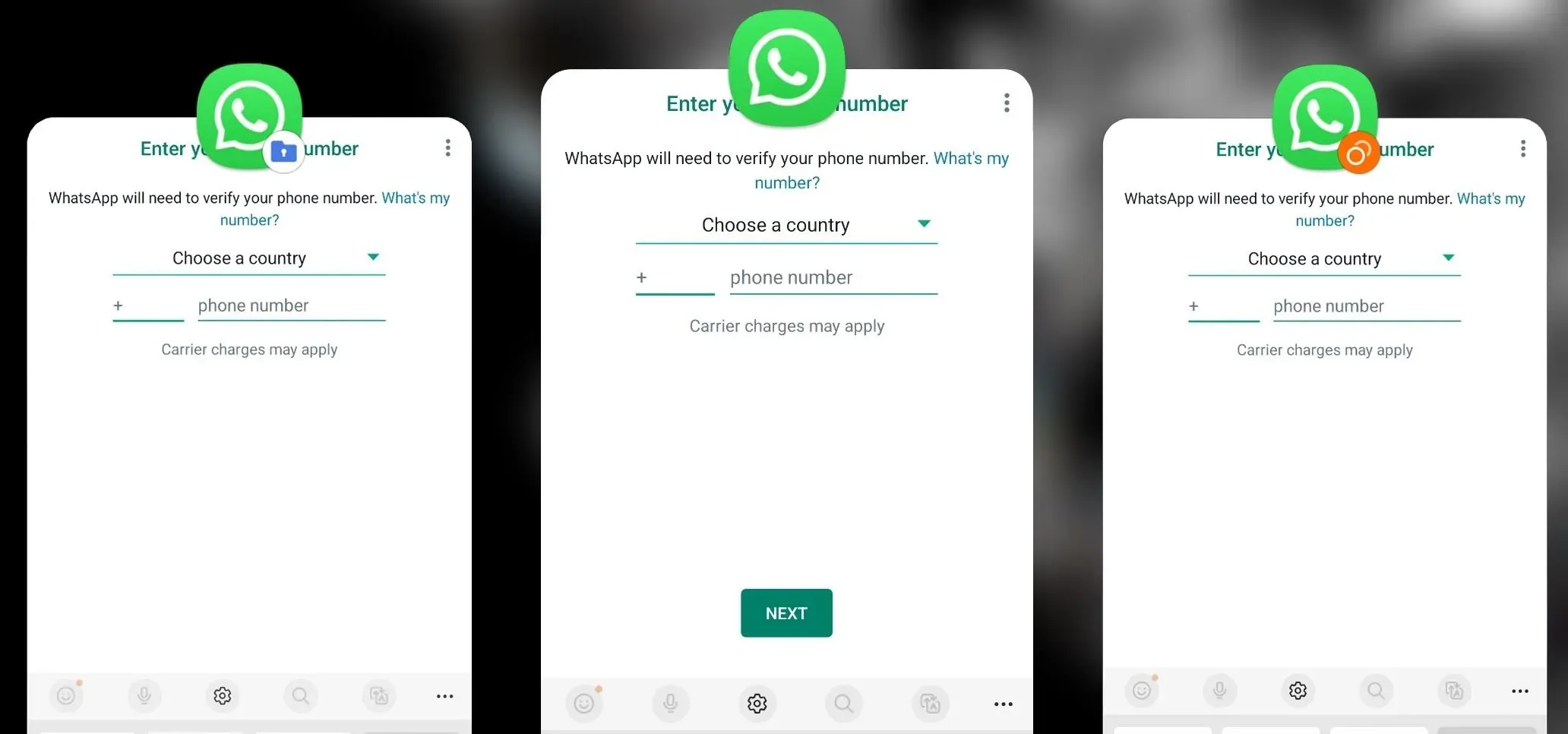
Productivity & Shortcuts







Featured On WonderHowTo:
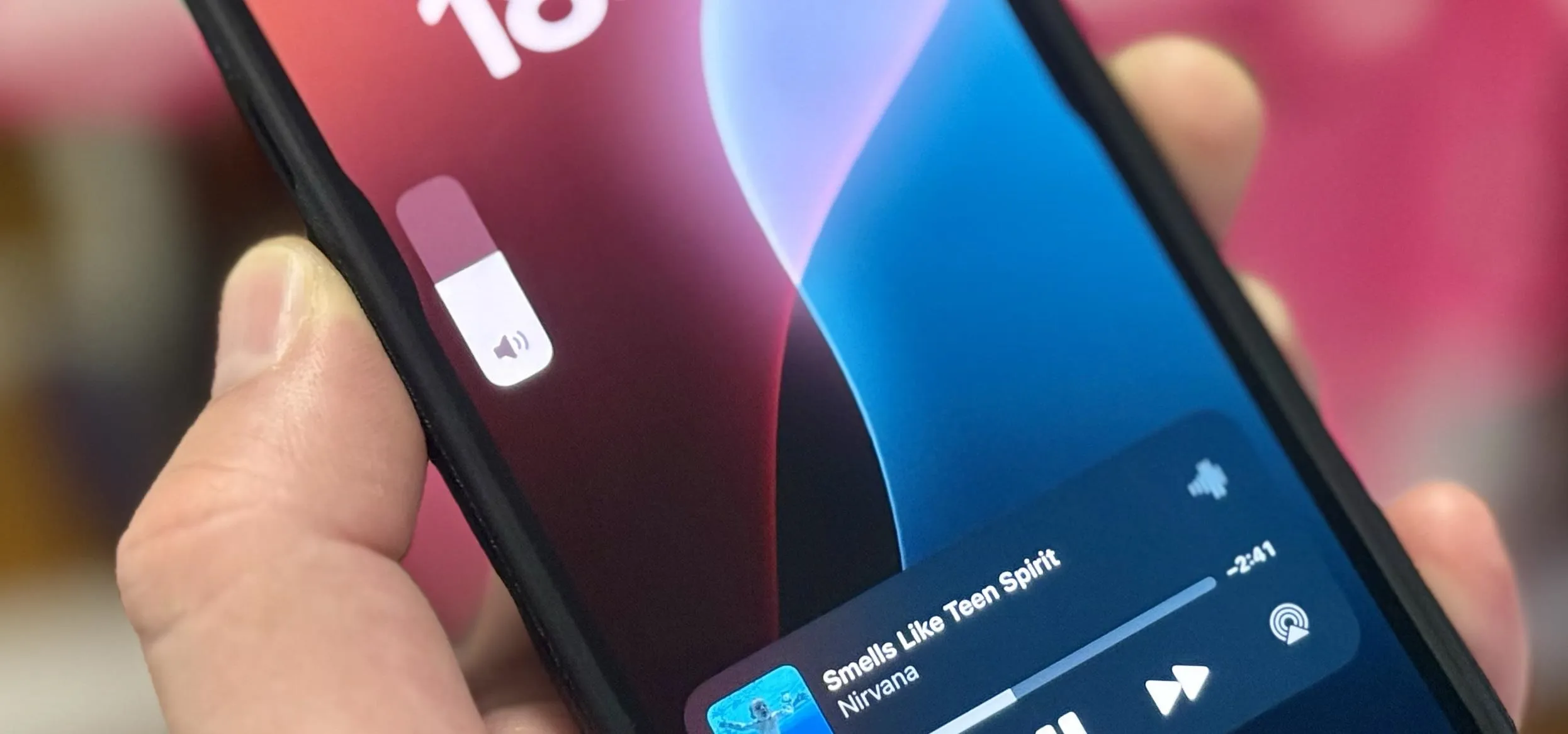
Music & Audio






Featured On WonderHowTo:
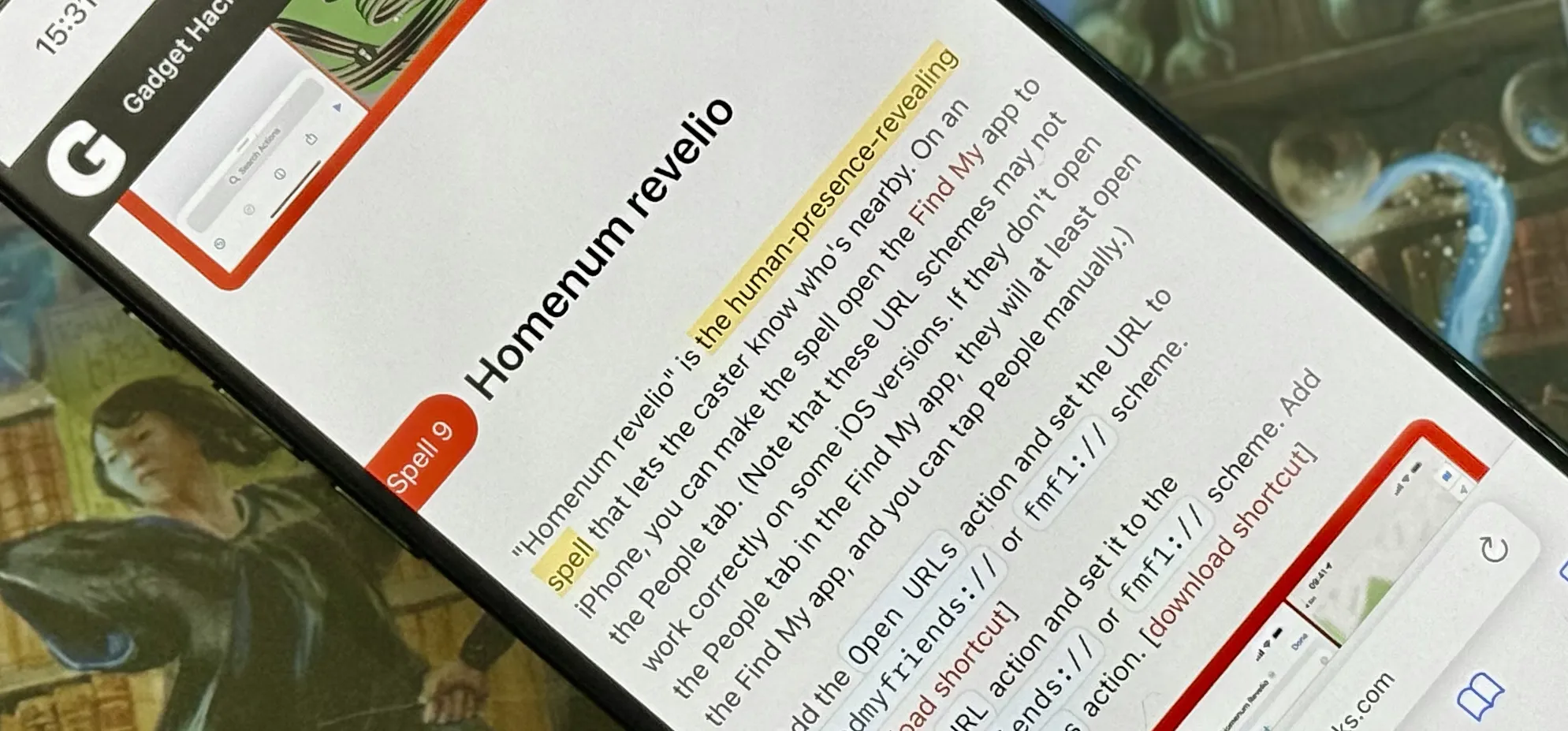
Augmented Reality






Featured On WonderHowTo:
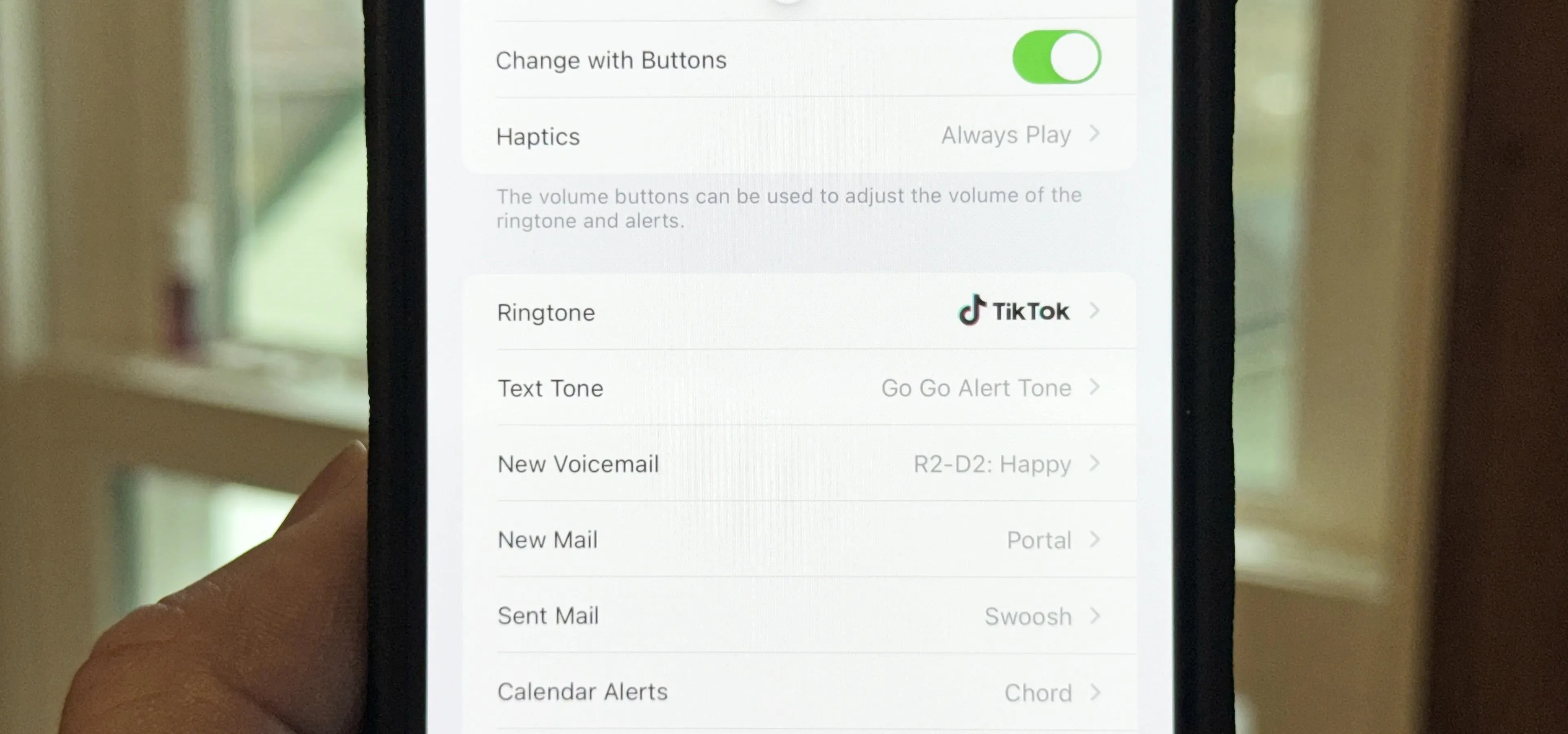
Gaming










news
Origami Panda